[Python] 속도 개선 - 알고리즘편
- Python/알고리즘
- 2021. 9. 12.
알고리즘을 구성했을 때 파이썬에서 속도 개선을 위한 시도입니다.
어느 알고리즘을 하느냐에 따라 속도 차이는 있을 수는 있습니다.
알고리즘 이론에서 배우는 복잡한 알고리즘 말고 간단한 알고리즘으로
이전 포스팅에서 얘기한 속도 개선방안 중 어느 것이 효율적인지 확인해보도록 하겠습니다.
알고리즘은 소수 찾는 방법을 만들건데 메르센소수나 페르마 소수 같은 수학 지식이 들어간 방법 말고
소수의 정의대로 알고리즘을 만들어서 시도를 하겠습니다.
소수는 1과 자기자신으로만 나누어지는 숫자를 의미합니다. 예로 2,3,5,7 이런 수가 있습니다.
숫자가 작으면 금방 소수인지를 알아낼 수 있지만 숫자가 커지면 굉장히 어려워집니다.
소수를 찾는 규칙이 따로 존재하면 규칙을 사용하면 되지만 현재로서는 그런 규칙은 부분적으로만 있고 전체적으로는 없어서 규칙으로는 찾아낼 수가 없습니다.
그래서 컴퓨터에게 노동을 시켜서 찾아보는 수행을 하고자 할텐데 계산이 빨라야 큰 수를 다룰 수 있게 됩니다.
이런 관점으로 파이썬에서 어떤 방법으로 하는게 효율이 알아보고자 하는 단순 호기심 포스팅입니다.
알고리즘 구성
일단 짝수는 모두 2를 약수를 가집니다. 그래서 2를 제외하고는 모두 소수가 될 수 없습니다.
따라서 찾고자 하는 숫자를 x라고 하면 짝수인지를 확인을 하고
홀수이면 x보다 작은 홀수마다 하나씩 나누기를 해서 나누어지는지 확인합니다.
범위를 1,2는 필요가 없고 (3, x-1)까지 하면 비효율적입니다.
정수론에 있는 $ \sqrt{x} $ 의 정수부분보다 작은 수중에 소인수가 존재한다는 정리를 사용하면 범위를 줄일 수 있어서 사용하겠습니다.
예를 들어, 15면 약수가 1,3,5,15로 $ \sqrt{15} $ 범위 안에 있는 숫자인 3으로 나누는 걸 알 수 있습니다.
5는 범위에 안 들어가지는데 이건 모두를 찾고자 하는 정리가 아니고 존재에 대한 정리이고
3 하나를 찾으면 5도 당연히 나오게 되어 쌍으로 찾게 되어서
적은 수에서 찾아 안 되면 큰 수도 안 될것이기 때문에 소수를 찾는데 큰 무리는 없어보입니다.
이것의 대한 증명은 심심하면 각자 알아서 하는걸로 하고 어쨋든 범위는 (0, $ \sqrt{x} $)의 홀수로 해서 양을 줄이도록 합니다.
정리하면 다음과 같습니다.
1. x가 홀수,짝수인지 확인
2. x가 홀수이면 범위 (3,$ \sqrt{x} $)의 홀수로 나누어 본다.
3. 나누어지면 소수가 아니고 모든 수로 나눌수 없다면 소수가 된다.
소수이면 True 라 출력 아니면 False 출력
이렇게 하는 단순한 알고리즘입니다.
Python
Python만 가지고 알고리즘을 구현해봅시다.
def is_prime(x):
if x % 2 ==0:
return False
for i in range(3,int(x**0.5)+1,2):
if x % i == 0:
return False
return True
x = int(1e10+3)
is_prime(x)
x를 지정하면 소수인지 아닌지 구분하는 함수를 만들었고 제가 넣은 숫자는 소수가 아닌가봅니다.
시간을 측정해보겠습니다.
%timeit is_prime(x)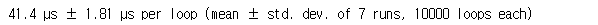
41.1 마이크로초로 굉장히 빠른걸 볼 수 있습니다.
소수 알고리즘은 벡터화할 이유가 없기 때문에 Numpy로 할 수 있는게 없어서 하지 않고 Numba로 시도를 해보겠습니다.
Numba
Numba는 캐싱해서 쓰는 방법이니 두번째 실행부터 진짜 속도입니다.
첫번째 시도입니다.
import numba as nb
is_prime_nb = nb.jit(is_prime)
%timeit is_prime_nb(x)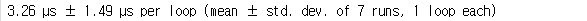
두번째 시도입니다.
%timeit is_prime_nb(x)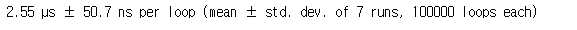
Numba를 쓰니 훨씬 빨라졌습니다.
Cython
Cython으로 시도합니다.
%load_ext Cython
%%cython
def is_prime_cython(x):
if x % 2 ==0:
return
for i in range(3,int(x**0.5)+1,2):
if x % i == 0:
return False
return True같은 함수인데 구분을 위해서 is_prime_cython으로 함수를 만들고 Cython으로 돌려보겠습니다.
%timeit is_prime_cython(x)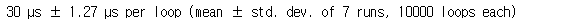
Cython이 Python보다는 빨라지긴 하는 것 같지만 Numba보다는 안 되는 것 같습니다.
Numba만큼 나오기 위해서 변수 x와 i의 타입을 static type으로 바꾸어서 진행해보겠습니다.
%%cython
def is_prime_cython2(long x):
cdef long i
if x % 2 ==0:
return False
for i in range(3,int(x**0.5)+1,2):
if x % i ==0:
return False
return Truestatic 타입으로 함수를 바꾸었습니다.
%timeit is_prime_cython2(x)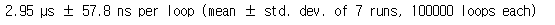
static으로 바꾸었더니 numba만큼 나오는 걸 볼 수 있습니다.
속도 개선이 확실히 되었습니다.
결론
당연하겠지만 Python이 가장 느린 속도를 가지고 있다는 것을 알 수 있었습니다.
두가지 방법만 시도를 해보았지만 Numda로 하는 것이 가장 간단하고 빠르고 Cython이 그 다음이었습니다.
그래도 Cython으로 Numba만큼의 속도를 가져올 수 있다는 걸 알 수 있었던 것 같습니다.
관련 포스팅
[Python/알고리즘] - [Python] 속도 개선 방법
[Python/알고리즘] - [Python] 속도 개선 -Loop편
'Python > 알고리즘' 카테고리의 다른 글
| [Python]속도개선 - Recursive pandas (0) | 2021.09.18 |
|---|---|
| [Python] 속도개선 -알고리즘편(Recursive) (0) | 2021.09.16 |
| [Python] 속도 개선 -Loop편 (0) | 2021.09.09 |
| [Python] 속도 개선 방법 (6) | 2021.09.04 |
| 더블 링크드 리스트(Double linked list) (0) | 2021.01.27 |