[Python] 속도개선 -알고리즘편(Recursive)
- Python/알고리즘
- 2021. 9. 16.
Recursive algorithm의 경우에 대해 알아보겠습니다.
이전 포스팅에서 numba와 cython을 가지고 속도 개선을 했는데 Recursive algorithm은 통하지 않습니다.
그 이유와 개선 방법에 대해 설명하겠습니다.
참고로 현재 속도개선에 관한 포스팅은 python for finance라는 책을 참고해서 포스팅하고 있습니다.
그런데 책대로 해도 다 되는 건 아니라서 여기저기 참고하면서 블로그에 정리를 하고 있습니다.
이러면서 공부가 되는거겠죠? 아무튼 정리의 목적이 크니 알아두셨으면 합니다.
Recursive algorithm
재귀라고 하는 방법입니다. 고등학교 수학시간에 수열에서 배운 점화식을 얘기합니다.
함수를 만들면 만든 함수를 이용해 다음 수를 계산하는 방법입니다.
예로 팩토리얼을 들 수 있을 것 같습니다.
팩토리얼을 코딩으로 만들 때 주로 재귀함수를 만듭니다.
밑의 코드 작성한걸 보면 n*facto(n-1)로 return을 하고 있습니다.
함수 안에 다시 함수가 들어가는 형태를 띄게 됩니다.
def facto(n):
if n ==1:
return 1
else:
return n*facto(n-1)
facto(3)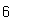
이 방법을 코딩으로 가져와서 많이 하는데 효율적이진 않습니다. 메모리를 많이 사용해야 하기 때문이죠.
그렇다고 반복문만 할 수도 없고 재귀를 써야하는 경우도 생겨서 재귀를 안 쓸 수도 없는 입장입니다.
그래서 꼬리 재귀를 써서 해결을 합니다. 꼬리 재귀는 연산을 하지 않고 결과만 출력하는 방식인데
문제는 다른 언어에서는 꼬리 재귀를 할 수 있지만 파이썬에서는 지원되지 않습니다.
Recursive 계산
그래서 이번 포스팅에서는 파이썬에서 피보나치 수열을 가지고 개선을 해보겠습니다.
피보나치는 다들 아니깐 설명은 생략하겠습니다.
단순하게 피보나치를 Recursive로 만들면 다음과 같이 만들 수 있습니다.
def fib_rec_py(n):
if n<2:
return n
else:
return fib_rec_py(n-1)+fib_rec_py(n-2)
fib_rec_py(6)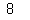
6번째 숫자인 8이 출력되었습니다.
이걸 큰수로 넘기면 시간이 많이 걸리게 됩니다. 간단하게 표시하기 위해 n번째 숫자를 F(n)이라고 하겠습니다.
F(10)을 예로 들면 위의 함수처럼 계산을 하게 되면 F(8)+F(9)를 해야합니다.
그리고 F(9)를 구하기 위해 F(8)+F(7)를 합니다. F(7)도 마찬가지겠죠.
그러면 F(9) 하나를 계산하기 위해서는 F(8)와 F(7)를 찾아내야 합니다.
거기다가 각기 함수로 호출했기 때문에 F(6)는 F(8)에서 한번, F(7)를 찾아내는데 한번으로 두번 계산하게 됩니다.
그래서 큰 숫자가 되면 계산양이 어마어마해집니다.
F(4)만 보면 총 10번의 계산을 하게 됩니다. F(5),F(6),F(7),F(8)도 계산해야하니 계산량이 늘어납니다.

한마디로 어마어마하게 비효율적입니다.
속도 개선
속도 개선을 위해 numba와 cython을 써보긴 하겠지만 구조상 큰 개선은 안되겠지만 해보겠습니다.
Pure python
%timeit fib_rec_py(30)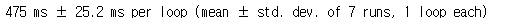
Numba
Numba를 쓰면 캐싱 문제로 한번 오류가 나올 수 있는데 무시하고 진행합니다.
아래 코드는 2번째 돌린 결과입니다.
import numba as nb
fib_rec_nb = nb.jit(fib_rec_py)
%timeit fib_rec_nb(30)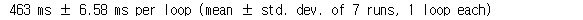
Cython
%load_ext cython
%%cython
def fib_rec_cy(int n):
if n<2:
return n
else:
return fib_rec_cy(n-1)+fib_rec_cy(n-2)
%timeit fib_rec_cy(30)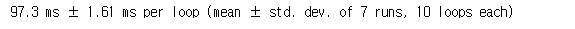
Cython을 이용하면 상대적으로 빨라지긴 하지만 절대적으로 빠른편은 아닙니다. 30번째 수를 구하는데 97.3 밀리초이면 빠른 건 아닙니다.
구조 해결(계산량 줄이기)
구조를 해결해서 파이썬으로 속도 개선으로 해보겠습니다.
현재 Recursion의 문제는 계산 반복입니다. 계산을 반복하지만 않으면 속도가 굉장히 빨라질 것이기 때문에 계산을 줄이는 시도를 해야합니다. 미리 값을 저장한다면 개선이 될 것입니다.
Memoization
첫번째 방법으로 Memoization 이라는 방법을 씁니다.
방법을 간단히 설명하면 dict을 만들어서 거기에 임시로 저장해서 꺼내쓰는 방법입니다.
아래 코드처럼 함수를 정의할 수 있습니다.
cache = dict()
def fib(n):
if n in cache:
return cache[n]
if n==0:
x = 0
elif n==1:
x = 1
else:
x = fib(n-1) + fib(n-2)
cache[n] = x
return x
시간을 재보겠습니다.
%timeit fibonacci(30)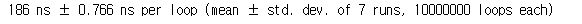
186 나노초까지 빨라지는 걸 볼 수 있습니다.
functools lru_cache
다음은 decorator를 사용하는 방식입니다. decorator는 말그대로 구조에다 기능을 추가하는 방법입니다.
피보나치의 문제는 cache가 안되서 계산을 반복하는 것이었는데 구조를 그대로 재사용을 하면서 cache 보존을 한다면 계산량을 줄일 수 있으니 속도가 빨라질 겁니다. 다행히도 lru_cache라는 모듈이 있어서 그것을 사용하면 됩니다.
이를 decorator에 붙입니다.
decorator는 @추가기능 을 써넣은 후 코드진행을 하면 됩니다.
from functools import lru_cache as cache
@cache(maxsize=None)
def fib_rec_py2(n):
if n<2:
return n
else:
return fib_rec_py2(n-1)+fib_rec_py2(n-2)
@cache로 함수에 기능장착을 시켰습니다.
%timeit fib_rec_py2(30)
lru_cache를 쓰니 깔끔하면서도 속도도 개선이 된 것을 볼 수 있습니다.
결론
재귀함수는 파이썬에서 구현하기엔 좋지 않아보입니다. 그래도 decorator나 memoization을 이용해 속도 개선을 할 수 있다는 걸 알 수 있었습니다.
사실, 편하게 C++ 하면 되지만 코드전체를 재귀함수로 도배를 할 건 아니고 앞서 보인 numpy의 계산을 통해서도 C 못지 않는 속도가 나오면서 간단히 구현할 수 있는 장점이 있으니 제 생각에는 C와 병행하면서 쓰는 게 좋지 않을까 싶습니다.
관련 포스팅
Python/알고리즘] - [Python] 속도 개선 방법
[Python/알고리즘] - [Python] 속도 개선 -Loop편
[Python/알고리즘] - [Python] 속도 개선 - 알고리즘편
참고문헌
Python for finance
https://pythoninformer.com/programming-techniques/functional-programming/recursion/
'Python > 알고리즘' 카테고리의 다른 글
| [파이썬 자료구조] 해쉬테이블 구현해보기 (0) | 2022.12.22 |
|---|---|
| [Python]속도개선 - Recursive pandas (0) | 2021.09.18 |
| [Python] 속도 개선 - 알고리즘편 (0) | 2021.09.12 |
| [Python] 속도 개선 -Loop편 (0) | 2021.09.09 |
| [Python] 속도 개선 방법 (6) | 2021.09.04 |