zk-SNARKs 다항식과 타원곡선의 수학
- 수학/수학이야기
- 2025. 8. 12.
zk-SNARKs 다항식과 타원곡선의 수학
"100만 개의 복잡한 계산을 단 192바이트로 압축할 수 있다면?"
이것이 바로 zk-SNARKs가 해결하는 문제입니다. 1편에서 본 알리바바 동굴의 간단한 영지식 증명과는 차원이 다른, 실용적이고 확장 가능한 영지식 증명 시스템입니다.
오늘은 zk-SNARKs의 핵심인 QAP(Quadratic Arithmetic Programs)와 타원곡선 쌍함수(Elliptic Curve Pairing)를 깊이 있게 분석해보겠습니다. 이 기술들이 어떻게 결합되어 현대 블록체인의 프라이버시와 확장성 문제를 해결하는지 살펴보겠습니다.
🎯 zk-SNARKs: 실용적 영지식 증명의 구현
SNARKs의 의미와 기술적 특징
zk-SNARKs = Zero-Knowledge Succinct Non-interactive ARguments of Knowledge
각 구성 요소의 기술적 의미:
🔍 Zero-Knowledge (영지식)
증명 과정에서 비밀 정보가 전혀 노출되지 않음
시뮬레이터가 구별 불가능한 가짜 증명을 생성 가능
정보 이론적 또는 계산적 영지식성 보장
📏 Succinct (간결함)
증명 크기: O(1) - 상수 크기 (보통 192~288바이트)
검증 시간: O(1) - 상수 시간 (수 밀리초)
계산 복잡도와 무관하게 일정한 크기 유지
🚫 Non-interactive (비대화형)
증명자와 검증자 간 실시간 상호작용 불필요
한 번 생성된 증명은 언제든 검증 가능
블록체인에 저장하여 영구 보존 가능
⚖️ Arguments (논증)
계산적 건전성: 다항식 시간 공격자에 대해서만 안전
무한한 계산 능력으로는 이론상 깨질 수 있음 (실용적으로는 불가능)
암호학적 가정에 기반한 보안성
성능 비교 분석
전통적 영지식 증명 vs zk-SNARKs:
기존 방식:
- 증명 크기: 계산 복잡도에 비례 (MB~GB)
- 검증 시간: 원래 계산을 다시 실행
- 통신: 여러 라운드 필요
- 실용성: 제한적
zk-SNARKs:
- 증명 크기: 192바이트 (항상 일정)
- 검증 시간: 6밀리초 (항상 일정)
- 통신: 한 번의 메시지로 완료
- 실용성: 산업용 적용 가능
🔄 계산에서 회로로: R1CS 변환 과정
zk-SNARKs의 첫 번째 단계는 모든 계산을 표준화된 산술 회로로 변환하는 것입니다.
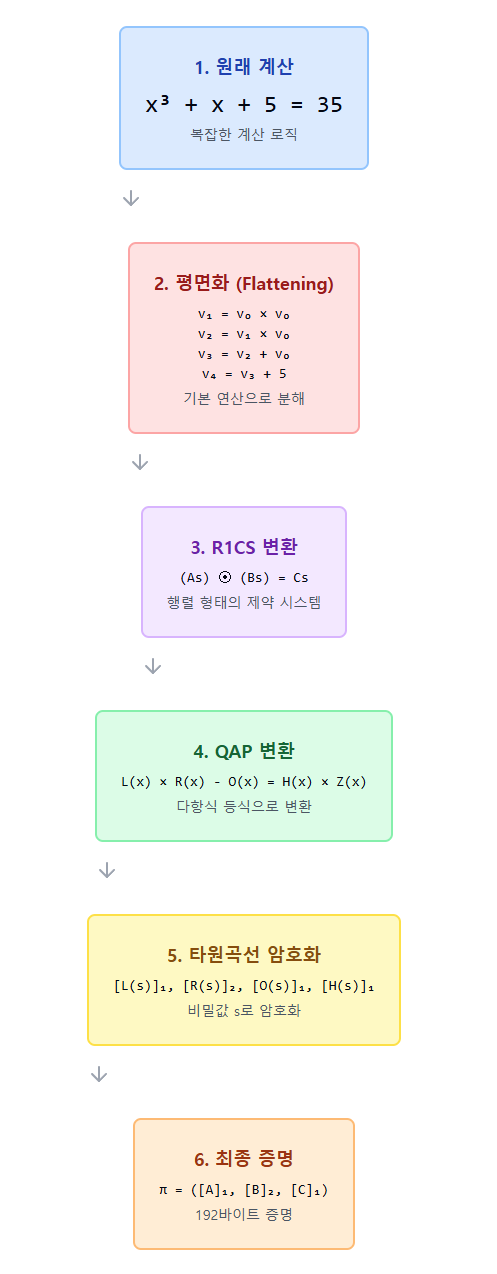
구체적 예제: x³ + x + 5 = 35
우리가 증명하고 싶은 명제: "나는 x³ + x + 5 = 35를 만족하는 x를 알고 있다"
1단계: 평면화(Flattening)
복잡한 식을 기본 연산들의 연쇄로 분해합니다:
원래 식: x³ + x + 5 = 35
평면화:
v₀ = x (입력 변수)
v₁ = v₀ × v₀ (x²)
v₂ = v₁ × v₀ (x³)
v₃ = v₂ + v₀ (x³ + x)
v₄ = v₃ + 5 (x³ + x + 5)
v₅ = 35 (목표 출력)
2단계: R1CS (Rank-1 Constraint System) 변환
각 제약을 A × B = C 형태로 표현합니다:
제약 1: v₀ × v₀ = v₁
제약 2: v₁ × v₀ = v₂
제약 3: (v₂ + v₀) × 1 = v₃
제약 4: (v₃ + 5) × 1 = v₄
제약 5: v₄ × 1 = v₅
행렬 표현
R1CS는 세 개의 행렬 A, B, C로 표현됩니다.
Witness 벡터
s = [1, v₀, v₁, v₂, v₃, v₄, v₅] = [1, 3, 9, 27, 30, 35, 35]
행렬 구조
A = [[0, 1, 0, 0, 0, 0, 0], # v₀
[0, 0, 1, 0, 0, 0, 0], # v₁
[0, 1, 0, 1, 0, 0, 0], # v₂ + v₀
[5, 0, 0, 0, 1, 0, 0], # 5 + v₃
[0, 0, 0, 0, 0, 1, 0]] # v₄
B = [[0, 1, 0, 0, 0, 0, 0], # v₀
[0, 1, 0, 0, 0, 0, 0], # v₀
[1, 0, 0, 0, 0, 0, 0], # 1
[1, 0, 0, 0, 0, 0, 0], # 1
[1, 0, 0, 0, 0, 0, 0]] # 1
C = [[0, 0, 1, 0, 0, 0, 0], # v₁
[0, 0, 0, 1, 0, 0, 0], # v₂
[0, 0, 0, 0, 1, 0, 0], # v₃
[0, 0, 0, 0, 0, 1, 0], # v₄
[0, 0, 0, 0, 0, 0, 1]] # v₅
검증 조건
(As) ⊙ (Bs) = Cs
여기서 ⊙는 요소별 곱셈(element-wise multiplication)
🎪 QAP: 다항식으로의 체계적 변환
R1CS에서 QAP로의 변환 원리
QAP의 핵심 아이디어는 R1CS의 각 열을 다항식으로 변환하는 것입니다.
라그랑주 보간법(Lagrange Interpolation) 활용합니다.
제약이 m개 있다면, 점 1, 2, ..., m에서 정의된 함수를 다항식으로 변환
예시: A 행렬의 첫 번째 열 [0, 0, 0, 5, 0]
→ 다항식 A₁(x)를 찾아서:
A₁(1) = 0, A₁(2) = 0, A₁(3) = 0, A₁(4) = 5, A₁(5) = 0
라그랑주 보간법의 수학적 구현
m개의 점 (x₁, y₁), (x₂, y₂), ..., (xₘ, yₘ)을 지나는 다항식
L(x) = Σ yᵢ × ℓᵢ(x)
i=1
여기서 ℓᵢ(x) = Π (x - xⱼ)/(xᵢ - xⱼ) (j ≠ i)
j≠i
구체적 계산 예시
점 (1,0), (2,0), (3,0), (4,5), (5,0)을 지나는 다항식
ℓ₄(x) = (x-1)(x-2)(x-3)(x-5) / ((4-1)(4-2)(4-3)(4-5))
= (x-1)(x-2)(x-3)(x-5) / (3×2×1×(-1))
= -(x-1)(x-2)(x-3)(x-5) / 6
A₁(x) = 5 × ℓ₄(x) = -5(x-1)(x-2)(x-3)(x-5) / 6
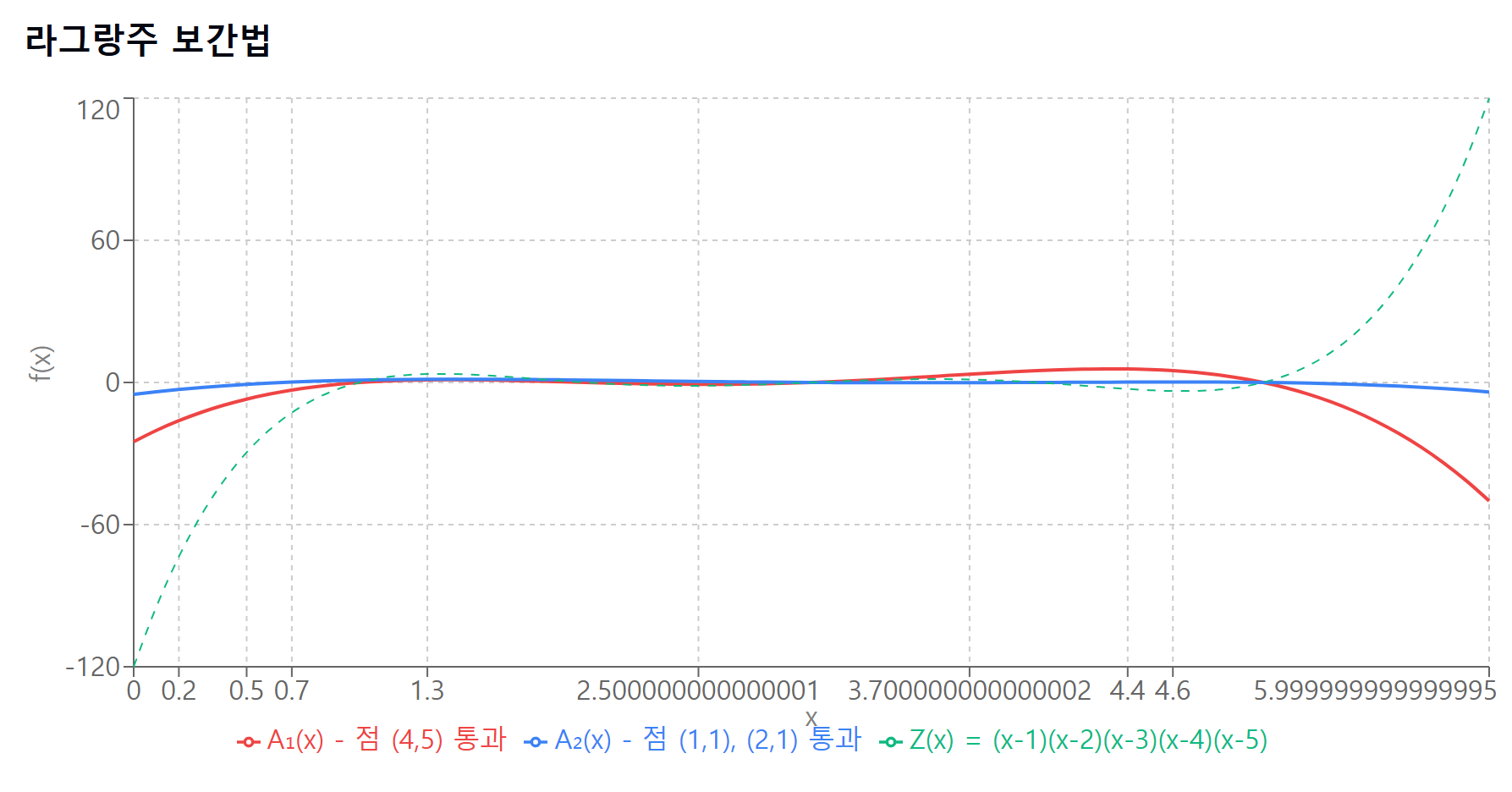
QAP의 핵심 수학적 성질
목표 다항식(Target Polynomial)
Z(x) = (x-1)(x-2)...(x-m)
QAP 조건
(Σ aᵢAᵢ(x)) × (Σ aᵢBᵢ(x)) - (Σ aᵢCᵢ(x)) = H(x) × Z(x)
여기서:
- aᵢ는 witness 벡터의 원소들
- H(x)는 몫 다항식(quotient polynomial)
분석 통찰 내역
- 좌변이 Z(x)로 나누어떨어진다면 모든 제약이 만족됨
- 나누어떨어지지 않으면 어딘가 제약 위반이 있음
- 다항식 나눗셈을 통해 일괄 검증 가능
효율성 분석
- m개의 개별 제약 → 1개의 다항식 등식
- 검증 복잡도: O(m) → O(1) (적절한 암호화 하에서)
🌟 타원곡선 쌍함수: 고급 암호학 도구
쌍함수(Pairing)의 수학적 정의
타원곡선 쌍함수는 두 개의 타원곡선 군에서 하나의 곱셈군으로의 매핑입니다:
e: G₁ × G₂ → Gₜ
핵심 성질 (쌍선형성):
e(aP, bQ) = e(P, Q)^(ab)
e(P₁ + P₂, Q) = e(P₁, Q) × e(P₂, Q)
e(P, Q₁ + Q₂) = e(P, Q₁) × e(P, Q₂)
BN254 곡선: 실용적 구현
Barreto-Naehrig 곡선 (254비트)
E: y² = x³ + 3 (mod p)
여기서 p = 36u⁴ + 36u³ + 24u² + 6u + 1
u = 4965661367192848881 (최적화된 시드 값)
실제 p = 21888242871839275222246405745257275088696311157297823662689037894645226208583
세 개의 군 구조
G₁: E(𝔽ₚ) - 기본 타원곡선 위의 점들
G₂: E'(𝔽ₚ²) - 2차 확장체 위의 곡선 점들
Gₜ: 𝔽ₚ¹² - 12차 확장체의 곱셈군
쌍함수를 이용한 QAP 검증
QAP의 다항식 등식을 타원곡선 위에서 검증하는 방법
원래 조건
L(s) × R(s) - O(s) = H(s) × Z(s)
타원곡선 변환 과정
1. 검증자가 비밀값 s를 선택하고 다음을 공개:
- [s]₁, [s²]₁, ..., [sᵈ]₁ ∈ G₁ (powers of tau)
- [s]₂, [s²]₂, ..., [sᵈ]₂ ∈ G₂
2. 증명자가 계산:
- [L(s)]₁ = Σ aᵢ[Aᵢ(s)]₁
- [R(s)]₂ = Σ aᵢ[Bᵢ(s)]₂
- [O(s)]₁ = Σ aᵢ[Cᵢ(s)]₁
- [H(s)]₁ = H(s) × [1]₁
쌍함수 검증
e([L(s)]₁, [R(s)]₂) = e([O(s)]₁ + [H(s)]₁ × [Z(s)]₁, [1]₂)
이것이 성립하면:
L(s) × R(s) = O(s) + H(s) × Z(s) ✅
보안성 분석
- 이산 로그 문제의 어려움에 기반
- 계산적 Diffie-Hellman 가정
- q-Strong Diffie-Hellman 가정
🔐 신뢰할 수 있는 설정 (Trusted Setup)
독성 폐기물(Toxic Waste) 문제
zk-SNARKs의 가장 중요한 제약사항이 신뢰할 수 있는 설정입니다
설정 과정
1. 비밀값 s, α, β, γ, δ 랜덤 생성
2. 검증 키와 증명 키 생성:
- [s^i]₁, [s^i]₂ (i = 0, 1, ..., d)
- [α]₁, [β]₁, [β]₂, [γ]₂, [δ]₁, [δ]₂
- 기타 특수 키들...
3. 비밀값들 완전 삭제 (독성 폐기물 제거)
위험성 분석
만약 s, α, β, γ, δ 중 하나라도 유출되면:
→ 가짜 증명 생성 가능
→ 전체 시스템 보안 붕괴
→ 암호화폐의 경우 무한 발행 가능
Powers of Tau 의식과 MPC
이 문제를 해결하기 위해 **다자간 계산(Multi-Party Computation)**을 사용합니다
Zcash의 Powers of Tau 과정
참여자 1: r₁ 선택, [r₁]₁, [r₁²]₁, ... 계산
참여자 2: r₂ 선택, [r₁r₂]₁, [(r₁r₂)²]₁, ... 계산
...
참여자 n: rₙ 선택, [r₁r₂...rₙ]₁, [(r₁r₂...rₙ)²]₁, ... 계산
최종 비밀값: s = r₁ × r₂ × ... × rₙ
보안 모델
n명 중 1명만 정직하면 전체 시스템 안전
모든 참여자가 담합해야만 시스템 공격 가능
실제로 Zcash는 200여명이 참여한 의식 진행
🎨 실제 구현: Groth16 프로토콜
현재 가장 널리 사용되는 Groth16 프로토콜의 구체적인 구조를 분석해보겠습니다.
증명 구조와 효율성
증명 π = ([A]₁, [B]₂, [C]₁)
세 개의 군 원소로만 구성된 간결한 증명!
증명 생성 과정
1단계: Witness 계산
공개 입력: x₁, x₂, ..., xₗ
비공개 입력: w₁, w₂, ..., wₘ
전체 witness: a = (1, x₁, ..., xₗ, w₁, ..., wₘ)
2단계: 랜덤성 추가
r, s ← 𝔽ᵣ (랜덤 선택)
3단계: 증명 계산
[A]₁ = α + Σ aᵢuᵢ + r·δ
[B]₂ = β + Σ aᵢvᵢ + s·δ
[C]₁ = (Σ aᵢwᵢ + h(x)·t(x) + A·s + B·r - r·s·δ) / δ
여기서:
- uᵢ, vᵢ, wᵢ는 QAP 다항식들의 암호화된 값
- h(x)는 몫 다항식
- t(x)는 목표 다항식
검증 과정
단 하나의 쌍함수 등식:
e([A]₁, [B]₂) = e([α]₁, [β]₂) × e(Σ xᵢ[IC_i]₁, [γ]₂) × e([C]₁, [δ]₂)
성능 지표:
- 증명 크기: 3 × 32바이트 = 96바이트
- 검증 시간: 1회 쌍함수 계산 ≈ 2-3ms
- 검증자 계산: O(|공개입력|) + O(1)
🏗️ 실제 응용: Zcash의 JoinSplit
Zcash의 수학적 구조
Zcash는 Groth16을 사용해 완전한 거래 프라이버시를 제공합니다:
증명하려는 명제:
"나는 유효한 거래를 실행했다"
구체적으로:
1. 입력 노트들의 유효성
2. 충분한 잔고 보유
3. 이중 지불 방지
4. 올바른 암호화
5. 머클 트리 멤버십
숨기려는 정보:
- 송신자 주소
- 수신자 주소
- 거래 금액
- 노트 내용
- 머클 경로
JoinSplit 회로의 복잡성 분석
회로 크기:
- 제약 조건 수: ~1.8백만 개
- 변수 수: ~1.4백만 개
- 증명 생성 시간: ~40초 (2018년 기준)
- 증명 크기: 192바이트
- 검증 시간: ~6ms
주요 컴포넌트별 제약 수:
1. SHA256 해시 (×4회) : ~150k 제약
2. 머클 트리 증명 (×2회) : ~64k 제약
3. 공개키 암호화 : ~50k 제약
4. 커밋먼트 계산 : ~30k 제약
5. PRF 계산 : ~20k 제약
6. 기타 로직 : ~나머지
🌊 최적화 기법들
벡터 커밋먼트 최적화
Kate-Zaverucha-Goldberg (KZG) 커밋먼트:
다항식 f(x) = Σ aᵢxᵢ에 대한 커밋먼트:
C = [f(s)]₁ = Σ aᵢ[sᵢ]₁
opening at point z:
π = [(f(s) - f(z))/(s - z)]₁
검증:
e(π, [s - z]₂) = e([C - f(z)]₁, [1]₂)
배치 검증 최적화
여러 증명을 한 번에 검증하는 기법:
개별 검증:
e(A₁, B₁) = e(α, β) × e(IC₁, γ) × e(C₁, δ)
e(A₂, B₂) = e(α, β) × e(IC₂, γ) × e(C₂, δ)
...
배치 검증:
e(Σ rᵢAᵢ, Σ rᵢBᵢ) = e(α, β)^(Σ rᵢ) × e(Σ rᵢIC₁, γ) × e(Σ rᵢCᵢ, δ)
여기서 rᵢ는 랜덤 가중치
성능 향상: n개 증명 검증을 80% 시간 단축
🔮 한계와 발전 방향
현재의 기술적 한계들
1. 신뢰할 수 있는 설정
- 회로마다 별도 설정 필요
- 독성 폐기물 위험성
- 투명성 부족
- 업그레이드 어려움
2. 회로 고정성
- 컴파일 타임에 회로 구조 결정
- 동적 로직 구현 어려움
- 범용성 제한
- 회로 크기 최적화 필요
3. 증명 생성 비용
- 높은 메모리 요구량 (GB 단위)
- 긴 증명 생성 시간 (초~분 단위)
- 전문 하드웨어 필요
- 배터리 소모 문제 (모바일)
차세대 기술 동향
Universal SNARKs
- PLONK: 공통 신뢰 설정 재사용
- Sonic: 업데이트 가능한 설정
- Marlin: 더 효율적인 유니버설 구조
- 회로 독립적 설정 가능
재귀적 SNARKs
- 증명의 증명 생성 가능
- 무한 압축 달성
- 실시간 검증 체인 구성
- 증명 크기 완전 상수화
하드웨어 가속
- GPU 최적화: 10-100배 속도 향상
- FPGA 구현: 전력 효율성 개선
- ASIC 개발: 전용 칩 설계
- 클라우드 증명 서비스
🎯 마무리: 수학적 정밀함이 만드는 실용성
zk-SNARKs는 현대 수학의 여러 분야가 수렴한 결과물입니다. 대수기하학, 수론, 암호학이 만나 실용적인 솔루션을 만들어냈습니다.
오늘 우리가 분석한 기술적 핵심
🔄 체계적 변환 과정
- 프로그램 → R1CS → QAP → 타원곡선 → 쌍함수
📐 다항식의 효율성
- 라그랑주 보간법으로 이산을 연속으로
- 나눗셈으로 제약 일괄 검증
- 차수로 복잡도 통제
🌟 쌍함수의 실용성
- 두 차원의 정보를 하나로 결합
- 암호화된 상태로 연산 수행
- 검증자의 계산 부담 최소화
🔧 현실적 고려사항
- 신뢰할 수 있는 설정의 필요성과 위험
- 회로 설계의 복잡성
- 성능과 보안의 트레이드오프
다음에 여러분이 Zcash로 익명 거래를 하거나, zk-Rollup을 사용할 때, 그 뒤에서 수천만 개의 제약 조건이 192바이트로 압축되는 정밀한 수학적 과정이 일어나고 있음을 이해하실 수 있을 것입니다.
zk-SNARKs는 순수 수학이 현실 문제를 해결하는 가장 인상적인 사례 중 하나입니다.
'수학 > 수학이야기' 카테고리의 다른 글
| [수치해석] 고차 다항식 보간의 함정: Runge 현상 이해하기 (4) | 2025.08.26 |
|---|---|
| zk-STARKs와 투명한 영지식의 세계 (14) | 2025.08.13 |
| 비밀을 말하지 않고 진실을 증명하기(feat.영지식 증명) (6) | 2025.08.11 |
| 디지털 서명의 수학 원리 (8) | 2025.08.09 |
| 암호화폐와 블록체인 속 수학 원리 (15) | 2025.08.08 |