[numpy] 행렬식, 고유값 계산하기(np.linalg)
- Python / Numpy
- 2021. 11. 6.
np.linalg을 이용해 행렬 계산을 해보겠습니다.
1. 행렬식(np.linalg.det(x))
행렬식을 구하는 방법입니다. 보통 행렬식이 0이 아니면 역행렬이 존재하므로 확인용으로 하거나
지금은 파이썬으로 할 것이라 역행렬을 구할 때 행렬식을 구하고 계산해서 쓰진 않을 거지만 실제 수학계산에서는
행렬식을 반드시 사용해주어야 합니다.
예로 2x2 행렬을 해보겠습니다.
2x2 행렬식이면 |abcd| = ad-bc 로 계산이 됩니다.
만약 (1232) 라면 행렬식은 -4가 나옵니다.
import numpy as np
array = np.array([[1,2],[3,2]])
np.linalg.det(array)
2. 역행렬(np.linalg.inv(x))
역행렬도 간단하게 구할 수 있습니다. 다만 n차 정방행렬(nxn) 행렬일 때만 존재하니 참고하시길 바랍니다.
위에서 보인 array로 역행렬을 구해보겠습니다.
np.linalg.inv(array)
확인한다면 AA−1=A−1A=I 로 할 수 있습니다. 즉, 서로 곱해서 단위행렬이 나온다면 됩니다. array.dot(inv_array)를 사용하면 확인할 수 있습니다.
inv_array = np.linalg.inv(array)
array.dot(inv_array)
float으로 설정해서 숫자가 복잡하게 나왔지만 (1001) 가 나오게 됩니다.
3. 고유값 고유벡터( eigenvalue, eigenvector = np.linalg.eig(x))
정방행렬 A에 대해, Ax=λx 이 성립하는 0이 아닌 벡터 x가 존재할 때 상수 λ 를 행렬 A의 고유값이라 하고 이 때의 x는 고유벡터라고 합니다.
손으로 계산하면 분수가 많이 나와 엄청난 시간을 소요하게 됩니다.
그렇지만 컴퓨터로 한다면 몇 초 안에 값을 구할 수 있습니다.
w를 eigenvalue로 v를 eigenvector로 하고 구하면 다음과 같습니다.
w,v = np.linalg.eig(array)
print(w)
array의 eigenvalue를 구하면 -1, 4로 두개로 나옵니다.
eigenvector는 두개인데 print를 하면 column 으로 나열되므로
하나씩 보려면 list처럼 인덱싱으로 불러내야 합니다.
print(v[:,0], v[:,1])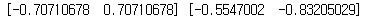
v[:,0] 은 -1에 대한 eigenvector 이고 v[:,1]은 4에 대한 eigenvector가 됩니다.
4. 선형연립방정식 해 구하기(np.linalg.solve(a,b))
np.linalg.solve() 를 이용해 AX=b 에 대한 식의 해를 구할 수 있습니다. 즉, X를 구하는 것입니다.
array를 다시 이용해 예제를 하나 만들어 구해보겠습니다.
x0+2x1=103x0+2x1=15 에서 x0,x1을 구합니다.
a = np.array([[1,2],[3,2]])
b = np.array([10,15])
x = np.linalg.solve(a,b)
print(x)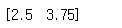
5. 최소제곱의 해 구하기(b,a = np.linalg.lstsq(A,y,rcond=None)[0])
최소 제곱의 해를 구하는 방법입니다. y = a+bx 일 때 , 데이터셋에 맞게 a와 b의 적합한 계수를 구합니다.
이때 x,y 는 주어집니다.
임의로 데이터셋 x,y를 만들어 최적의 계수를 찾아보겠습니다.
x = np.array([0,1,2,3])
y = np.array([1,3,5,7])
A = np.vstack([x,np.ones(len(x))]).T
b, a = np.linalg.lstsq(A,y,rcond=None)[0]
print(b,a)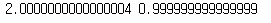
쉬운 예라서 눈으로 봐도 y = 2x+1 가 되어야 함을 볼 수 있습니다.
파이썬으로 계산해도 계수가 같은 값으로 나오는 것을 볼 수 있습니다.
함께 보면 좋은 글
[Numpy] 소수점 반올림하기(np.set_printoptions)
수치계산을 하다보면 반올림을 하거나 소수점 제한을 줘서 출력해야 하는데 numpy에서 그런 역할을 하는 메쏘드가 있습니다. np.set_printoptions라는 것인데요. 정밀화 과정을 하거나 표현을 쉽게 하
seong6496.tistory.com
'Python > Numpy' 카테고리의 다른 글
| [Numpy] 배열 분할하기(np.split) (0) | 2022.01.03 |
|---|---|
| [Numpy] 분포함수(distribution) (0) | 2021.11.20 |
| [Numpy] 소수점 반올림하기(np.set_printoptions) (0) | 2021.09.28 |
| [Numpy]ndarray 저장, 불러오기 (0) | 2021.06.15 |
| [Numpy]격자 그리드 만들기(meshgrid) (1) | 2021.05.19 |
데이터목장님의
글이 좋았다면 응원을 보내주세요!



