[Sympy] 파이썬으로 미분하기
- 수학
- 2021. 11. 17.
파이썬으로 미분할 때 Sympy를 사용하면 아주 편리합니다.
정의대로 미분
먼저 정의대로 되는지 구해보겠습니다.
미분의 정의는 순간속력을 알아내기 위한 방법으로 고안했습니다.
속력 = 거리/시간 인데 이를 그래프로 보면 속력은 기울기와 같게 됩니다.
예를 들어, a에서 b 시점까지의 평균속력은 a와 b 사이의 평균 기울기가 됩니다.
즉, 평균속력 = f(b)−f(a)b−a 이 됩니다.

관심을 갖는 건 a에서의 순간 속력입니다. 그러니 저 기울기가 a만 지나가야 하는 접선의 형태로 나타난다면 a의 순간속력이 될 것입니다.

이를 위해 limit를 도입합니다.
왜냐하면 속력 = 거리/시간 인데 b=a 가 되면 분수는 성립하지 않아서 속력을 구할 수 없게 됩니다.
그래서 a는 아니지만 a에 가까이 가는 b를 설정해 극한을 취한다면 숫자성립이 안 되는 분수를 피할 수 있게 됩니다.
이를 바탕으로 미분의 정의가 나왔습니다.
즉, 함수 f(x) 의 x= a 에서의 순간변화율은
f′(a)=limx→af(x)−f(a)x−a=limh→0f(a+h)−f(a)h
와 같습니다.
이제 이를 파이썬으로 구현해보겠습니다. 간단하게 2차함수로 하겠습니다.
f(x)=2x2+3x+6 의 미분을 정의를 이용해 구해보겠습니다.
import sympy as sy
x, a, h = sy.symbols('x a h')
f = 2*x**2 + 3*x + 6
fa = f.subs({x:a}) # f(a)
fh = f.subs({x:a+h}) # f(a+h)
sy.Limit((fh-fa)/h,h,0).doit() # f'(a)
대입을 하려면 subs({변수: 넣을값})를 이용합니다.
limit 결과값을 알기 위해 doit() 메쏘드를 썼습니다.
doit() 은 결과값을 식으로 출력해줍니다.
1변수 미분
변수가 하나인 경우 미분 방법입니다.
sin(x)+x 함수를 미분해보겠습니다.
import sympy as sy
x = sy.Symbol('x')
func = sy.sin(x)+x
func.diff()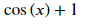
x에 특정한 값을 넣으려면 subs 안에 {변수 : 넣을값} 으로 딕셔너리를 만들거나 evalf(subs={변수:넣을값})으로 합니다.
2,3변수에서도 마찬가지 방법으로 합니다.
df.subs({x:0})
#또는
df.evalf(subs={x:0})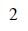
sympy에서는 미분함수도 하나의 식으로써 인지하기 때문에 방정식을 풀 수 있습니다.
예를 들어, f′(x)=1.5 을 만족하는 x를 구하고 싶다면 sy.nsolve()를 이용합니다.
x0 = sy.nsolve(df,1.5)
x0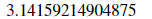
2변수 함수
2변수도 비슷합니다.
x, y 로 변수를 해서 미분을 하면 x로 미분하는 경우, y로 미분하는 경우로 나눠지는데 둘 다 모두 가능합니다.
f(x)=sin(x)+x+y+sin(y) 를 예로 해보겠습니다.
x, y = sy.symbols('x y')
f = sy.sin(x)+x+ y+ sy.sin(y)
df_x = sy.diff(f,x) # x에 대한 미분
df_y = sy.diff(f,y) # y에 대한 미분
print(df_x,',', df_y)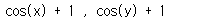
값을 대입하려면 1변수와 마찬가지로 subs를 이용합니다.
x, y 가 다 있는 f(x)를 예로 들면 다음과 같이 딕셔너리를 채워넣으면 됩니다.
f.subs({x:1.5, y: 1.5})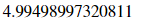
도함수에도 값 넣는게 가능하지만 1변수에서 한 방법과 동일하니 생략하겠습니다.
관련 포스팅
[수학] - [Sympy] 파이썬으로 수학식 만들기(기초연산)
[수학] - [미적분] 파이썬으로 적분하기(Integration)
'수학' 카테고리의 다른 글
| [sympy] 파이썬으로 함수 그래프 그리기 (0) | 2022.04.11 |
|---|---|
| [선형대] 정규방정식(Normal equation) (0) | 2021.12.15 |
| [Sympy] 파이썬으로 수학식 만들기(기초연산) (0) | 2021.11.14 |
| [미적분] 파이썬으로 적분하기(Integration) (0) | 2021.11.13 |
| [수치해석] 최소 제곱 방법(Least square approximation) (0) | 2021.10.29 |
데이터목장님의
글이 좋았다면 응원을 보내주세요!



