[미적분] 파이썬으로 적분하기(Integration)
- 수학
- 2021. 11. 13.
파이썬으로 적분을 하는 방법입니다.
적분에 대해 간단히 소개하면 적분은 면적을 구하는 방법으로 고대부터 연구된 분야입니다.
사각형이나 삼각형은 넓이를 구하는 방법은 잘 알려져 있습니다.
그리고 이를 활용해 직선으로 이루어진 도형에 대한 넓이를 구하는 방법을 알아낼 수 있습니다.
그런데 직선이 아닌 곡선으로 이루어진 도형은 사각형의 넓이를 구하는 방식으로는 구하기가 어렵습니다.
그럼에도 곡선으로 이루어진 도형을 구하기 위해 초반에는 직사각형의 넓이를 이용해 구분구적법이라는 방법으로 사용했습니다.
직사각형의 넓이가 밑변 x 높이 인 것을 알고 있었고 구하기 쉽기 때문에 곡선이 덮고 있는 면적을 수많은 직사각형으로 잘게 쪼개서 근사하는 방식으로 접근하는 방식입니다. 당연히 오차가 발생하고 계산량은 어마무시합니다.
이런 한계를 현대에 와서는 미적분의 기본정리를 바탕으로 구분구적법을 적분형식으로 변환해 계산방법도 다르게 되어 보다 정밀하면서도 쉬운 계산으로 면적을 구하는 것이 가능해졌습니다.
또한, 좌표평면에서 곡선을 그릴 수 있게 되어서 적분을 구하면 얻게되는 면적은 곡선과 x축까지의 면적으로 표준화되었습니다.
서론은 이쯤하고 바로 예제를 통해 파이썬으로 어떻게 그려지는지와 계산하는지 살펴보겠습니다.
수학적인 구체적인 설명은 따로 포스팅을 하도록 하겠습니다.
예는 ∫9.50.5f(x)dx=∫9.50.5sin(x)+xdx 입니다.
이 예는 python for finance 라는 책에서 약간 변형했습니다.
적분영역 그리기
적분영역을 그려보는 작업을 해보겠습니다.

위 그림처럼 그려내는게 목표입니다.
먼저 셋팅을 해야겠죠.
import scipy.integrate as sci
import numpy as np
def f(x):
return np.sin(x)+x
x = np.linspace(0,10) # x의 범위
y = f(x)
a = 0.5
b = 9.5
Inte_x = np.linspace(a,b) #적분할 x 범위
Inte_y = f(Inte_x) #적분할 y 범위
위 그림처럼 한다면 두개의 플롯을 하나에 그려낸다 생각하면 되겠습니다.
하나는 f(x)를 그려야 하고 다른 하나는 적분영역을 그려내야 합니다.
그래서 범위도 두개가 됩니다. f(x)의 영역과 적분영역이 되겠습니다.
그려보겠습니다!!
from matplotlib.patches import Polygon
from pylab import plt,mpl
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'
%matplotlib inline
fig, ax = plt.subplots(figsize=(10,6))
# f(x) 그리기
plt.plot(x,y,'b',linewidth=2)
plt.ylim(bottom=0)
# 적분영역 그리기
verts = [(a,0)]+list(zip(Inte_x,Inte_y))+[(b,0)] #리스트로 적분영역 범위지정
poly = Polygon(verts, facecolor='0.7', edgecolor='0.5') # polygon을 이용해 적분영역
ax.add_patch(poly) # poly 그리기
# 글자 삽입
plt.text(0.75*(a+b),1.5, r"$\int_a^b f(x)dx$", horizontalalignment='center',fontsize=20)
plt.figtext(0.9,0.075,'$x$')
plt.figtext(0.075,0.9,'$f(x)$')
ax.set_xticks((a,b))
ax.set_xticklabels(('$a$','$b$'))
ax.set_yticks([f(a),f(b)]);
Polygon 를 이용해 적분영역을 그려냈습니다.
(x,y)로써 표현해서 데이터를 올려주어야 해서 verts라는 리스트를 만들었고 ax에 붙여주었습니다.
쥬피터에서는 latex 지원이 가능해서 수학기호는 latex로 처리하였습니다.
축 글자는 figtext(x,y,글자) 로 하였고 파라미터 x,y는 좌표가 되겠습니다.
내가 원하는 좌표를 넣으면 위와 같이 x와 f(x) 을 지정된 좌표에 나오게 할 수 있습니다.
a,b는 set_xticks로 설정하였고 f(a),f(b) 값을 set_yticks에 넣어 나오게 했습니다.
적분 계산하기
이번에는 적분을 계산하는 방법입니다.
sympy를 써서 해보겠습니다.
sympy는 실제 수학하듯이 x를 미지수로 실제로 잡아서 진행하는 라이브러리인데
구체적인 방법은 따로 포스팅을 하겠습니다.
기초가 필요한 라이브러리는 아니니 금방 따라할 수 있을 겁니다.
위의 그림을 보면 알겠지만 숫자가 딱 떨어져 나오지 않을 거라는 건 짐작하실 것입니다.
정확하게 계산할 수 있는 것 하나를 놓고 다른게 맞는지 확인해보고 짧고 간결하게 코딩할 수 있는 것을 쓰면 되지 않나 싶어서 직관적인 것으로 결과를 구한 후 간결한 걸로 같은 값이 나오는지 비교를 해보겠습니다.
일단 미적분의 기본정리에 의해 정적분을 하면 ∫9.50.5f(x)dx=F(9.5)−F(0.5) 이 됩니다.
먼저 이걸 이용해 적분을 해보겠습니다. 계산 과정을 하나씩 보는거니깐 그나마 믿음이 갈 것 같습니다.
일단 셋팅을 해보겠습니다. 각 문자를 symbols() 를 이용해 변수로 인식하게 했습니다.
symbol 지정은 각각 가능하고 언패킹으로도 가능합니다.
import sympy as sy
a, b = sy.symbols('a b')
x = sy.symbols('x')
y = sy.symbols('y')
I = sy.Integral(sy.sin(x)+x,(x,a,b))
print(sy.pretty(I))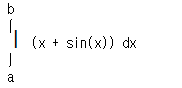
잘 되었다면 이런 형식 비슷한게 프린트됩니다.
명령어를 보면 하나도 pretty 하지 않은데 pretty하게 나오겠다고 하는 것 같아 좀 그렇지만
변수가 잘 지정된 것을 볼 수 있습니다. 컴퓨터에서 적분식으로써 받아들인다는 정도로 알고 계시면 될 것 같습니다.
적분을 해서 Fb-Fa 를 시행하겠습니다.
int_func = sy.integrate(sy.sin(x)+x,x) #부정적분 생성(적분상수는 0)
# 값 넣어 계산
Fb = int_func.subs(x,9.5).evalf()
Fa = int_func.subs(x,0.5).evalf()
#적분 계산
Fb-Fa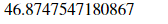
약 46.87 의 값이 나왔습니다.
다른 방법도 같은 값이 나오는지 확인해보겠습니다.
이 방법은 Fb-Fa로 하는 방법은 맞으나 Fb, Fa를 따로 구하지 않고 대입하는 형태입니다.
이것도 식으로써 표현이 가능하다는 것입니다.
식이 따로 필요할 수 있으니까요.
int_func_limits = sy.integrate(sy.sin(x)+x,(x,a,b))
print(sy.pretty(int_func_limits))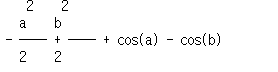
pretty를 하면 다음과 같이 Fb-Fa 형태로 구성된 것을 볼 수 있습니다.
a,b 에 값을 넣으면 적분값을 얻게 됩니다.
int_func_limits.subs({a:0.5,b:9.5}).evalf()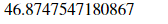
이런 거 모르겠고 한방에 적분시행하려고 한다면 다음과 같이 합니다.
sy.integrate(sy.sin(x)+x,(x,0.5,9.5))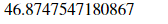
기본적인 내용을 포스팅을 하고 연결하는 형식으로 블로그를 쓰다보니 너무 느린 것 같아서 일단 모르더라도 따라할 수 있는 정도라 생각하고 마구 넣었습니다.
이전 포스팅에도 없는데 되어 있는 코딩의 자세한 사항과 내용은 추후에 차차 포스팅하도록 하겠습니다.
관련 포스팅
[Python/그래프 그리기] - [matplotlib]여러개로 나누어서 그래프 출력(subplot)
'수학' 카테고리의 다른 글
| [Sympy] 파이썬으로 미분하기 (0) | 2021.11.17 |
|---|---|
| [Sympy] 파이썬으로 수학식 만들기(기초연산) (0) | 2021.11.14 |
| [수치해석] 최소 제곱 방법(Least square approximation) (0) | 2021.10.29 |
| [수치해석] Spline interpolation(스플라인 보간법) (0) | 2021.10.23 |
| [수치해석] Equispaced interpolation(등간격 보간) (0) | 2021.10.20 |
데이터목장님의
글이 좋았다면 응원을 보내주세요!



