[Sympy] 파이썬으로 수학식 만들기(기초연산)
- 수학
- 2021. 11. 14.
파이썬에서 수학식을 세우는 라이브러리인 Sympy를 가지고 식을 만드는 간단한 방법을 소개하겠습니다.
파이썬이 객체지향언어다 보니 이런 것도 할 수 있나 싶어서 놀랍습니다.
직관적으로 수학식을 표현할 수 있어서 그 동안 배운 수학을 쉽게 코딩할 수 있는 것 같습니다.
수학에서도 미지수 x처럼 변수를 지정하고 문제를 풀어나가는데 Sympy에서도 마찬가지로 움직입니다.
그래서 Symbol() 함수를 이용해 변수를 지정하고 시작을 해야 오류가 발생하지 않습니다.
분수, 파이,복소수 ,변수 표시
분수는 sy.Rational(a,b)를 이용합니다. R을 반드시 대문자로 써야합니다.
sy.Rational(1,2)
파이같이 임의로 정해진 것도 쓸 수 있습니다.
sy.pi
수치화하고 싶다면 sy.N()으로 합니다. 또는 evalf()를 씁니다.
sy.N(sy.pi) # or sy.pi.evalf()
복소수는 대문자 I로 표시합니다.
sy.I
x,y를 변수로 지정해보겠습니다. 여러변수를 한꺼번에 하고 싶다면 sy.symbols()을
하나만 변수지정하고 싶다면 sy.Symbol()을 씁니다.
import sympy as sy
x ,y = sy.symbols('x y')
# 또는
x = sy.Symbol('x')
y = sy.Symbol('y')
type(x)
x를 type으로 보면 Symbol로 지정된 것을 볼 수 있습니다.
다항식 다루기
변수를 이용해 다항식을 만들어 보겠습니다.
f=x2+x+√x 라는 식을 만들어보겠습니다.
루트는 sy.sqrt() 로 표현할 수 있습니다.
f = x**2 + x + sy.sqrt(x)
f
식이 정리되어 있지 않다면 sy.simplify()를 이용해 정리하고 출력할 수 있습니다.
g = 1.2+2.5+x+x**2+ x**2
sy.simplify(g)
간단한 식은 전개도 가능합니다.
sy.expand((x-1)*(x-2))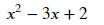
인수분해를 하고 싶다면 factor()를 사용합니다.
sy.factor(x**2-4)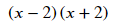
변수에 따른 항묶음을 하고 싶다면 sy.collect를 합니다.
ex = x**3 - 2*x*y +z**2+y**3 +4*x*z -3*y*z
ex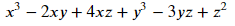
z로 묶어보겠습니다.
sy.collect(ex,z)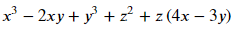
식.coeff()를 가지고 계수를 뽑아낼 수 있습니다.
ex.coeff(z)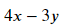
분수의 약분형태로 나타내고 싶다면 sy.cancel()을 사용합니다. 통분도 가능합니다.
ex = (x**2+4*x+4)/(x+2)
ex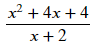
sy.cancel(ex)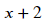
e = 1/x -2/x**2
sy.cancel(e)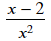
방정식 다루기
방정식을 만들고 싶다면 sy.Eq(좌변,우변)입니다.
sy.Eq(x**2,1)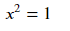
해를 구하고 싶다면 sy.solve()를 합니다. 괄호안에 풀고자 하는 식을 넣으면 됩니다.
다항식으로 넣어도 괜찮습니다.
a = sy.Eq(x**2,1)
sy.solve(a)
# 또는
sy.solve(x**2-1)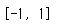
연립 방정식의 해를 구하려면 식 여러개를 넣어서 풉니다.
가령, x−y+6=0,3x+2y−3=0 이라는 연립방정식을 풀고 싶다면 다음과 같이 합니다.
sy.solve( [ x-y+6, 3*x+2*y-3 ], [x,y] )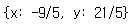
Taylor 급수
taylor 급수로 표현이 가능합니다.
sy.series(sy.sin(x), x )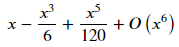
뒤에 따라나오는 오차표시인 O(x6) 을 지우고 싶다면 removeO()를 붙입니다. 여기서 O는 대문자 o 입니다.
sy.series(sy.sin(x), x ).removeO()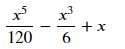
n파라미터를 추가해 항의 갯수를 조절할 수 있습니다.
sy.series( sy.sin(x), x, n=15 )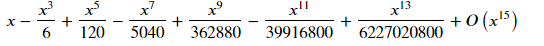
이상으로 기초계산에 대한 포스팅이었습니다.
미분, 적분과 행렬계산은 내용과 함께 sympy를 사용해 포스팅을 하겠습니다.
관련 포스팅
'수학' 카테고리의 다른 글
| [선형대] 정규방정식(Normal equation) (0) | 2021.12.15 |
|---|---|
| [Sympy] 파이썬으로 미분하기 (0) | 2021.11.17 |
| [미적분] 파이썬으로 적분하기(Integration) (0) | 2021.11.13 |
| [수치해석] 최소 제곱 방법(Least square approximation) (0) | 2021.10.29 |
| [수치해석] Spline interpolation(스플라인 보간법) (0) | 2021.10.23 |
데이터목장님의
글이 좋았다면 응원을 보내주세요!



