[미적분] 복리계산법
- 수학
- 2023. 7. 15.
자연대수 e를 이용한 복리법
복리법은 복리법인데 난데없이 자연대수 e을 가져다쓰는 어그로에 적잖이 의문을 가질 것 같습니다. 하지만 잘 따져보면 e가 복리 성질이 있는 것의 모델링을 할 때 굉장히 중요하다는 것을 느낄 수 있습니다.
일반적인 복리계산법
일반적으로 알려진 복리계산법은 다음과 같습니다.
원금 A, 이자 r, 주기 n, 기간 t일 때, 원금에 대한 복리는
A(1+r/n)nt
입니다.
예를 들어, 1000달러에 연이자 6% 이자갱신 주기가 하루인 복리상품을 3년동안 저축한다고 하면 3년 후에는 다음을 받게 됩니다.
1000(1+0.06/365)365∗3=1197.19
으로 약 1197.2 가 됩니다.
여기서 알 수 있는건 n이 증가할 때마다 지급되는 이자 또한 증가하는 것을 알 수 있습니다. 이 사실에 극한을 적용시키면 지속적으로 이자를 가중시킬 수 있습니다. 즉, n−>∞ 일 때, 최대 투자의 가치로 극대화한 값이라고 할 수 있습니다.
자연상수 e를 이용한 복리법 식
자연상수 e를 사용해 복리법을 바꿔보겠습니다.
자연상수 e의 정의에 대한 얘기는 다음 포스팅을 참고해주세요.
[미적분] 자연상수 e의 정의
자연로그의 밑 e 자연상수 e 또는 자연로그의 밑 e라고 불리는 수로 수학에서 π 와 함께 가장 자주 쓰는 상수라고 할 수 있습니다. 자연상수 e는 전혀 자연스럽게 생긴 수가 아닙니다. 어떤 필
seong6496.tistory.com
e를 이용해 다음과 같이 투자의 가치를 측정하는 함수를 만듭니다.
A(t)=limn−>∞A(1+r/n)nt
=A[limn−>∞(1+r/n)n/r]rt
=A[limm−>∞(1+1/m)m]rt(m=n/r)
=Aert
따라서, A(t)=Aert 입니다.
위에서 보인 예를 그대로 가져와서 해보면, A = 1000달러, 연이자 r= 6%를 3년동안 저축할 때 3년 후에 받는 양입니다.
A(3)=1000e0.06∗3=1197.21736312
으로 비슷한 양이 나옵니다.
파이썬으로 두 식의 비교
실제로 파이썬으로 값이 얼마나 다른지 살펴보겠습니다.
import math
import numpy as np
import matplotlib.pyplot as plt
interest_list = np.array([])
e_interest_list= np.array([])
for t in range(0,100):
interest = 1000*(1+0.06/365)**(365*t)
interest_list= np.append(interest_list,[interest],axis=0)
e_interest = 1000*math.exp(0.06*t)
e_interest_list= np.append(e_interest_list,[e_interest],axis=0)float은 list에 담을 수 없으니 numpy를 이용해 100년까지의 숫자를 담아보겠습니다.
mathploylib를 이용해 그래프를 두개를 그려봅니다.
plt.subplot(211)
plt.plot(interest_list)
plt.subplot(212)
plt.plot(e_interest_list,'r')
얼추 비슷하게 나오는 걸 볼 수 있습니다. 실제로 합쳐보면 확실하게 보입니다.
plt.plot(interest_list,'r')
plt.plot(e_interest_list,'o')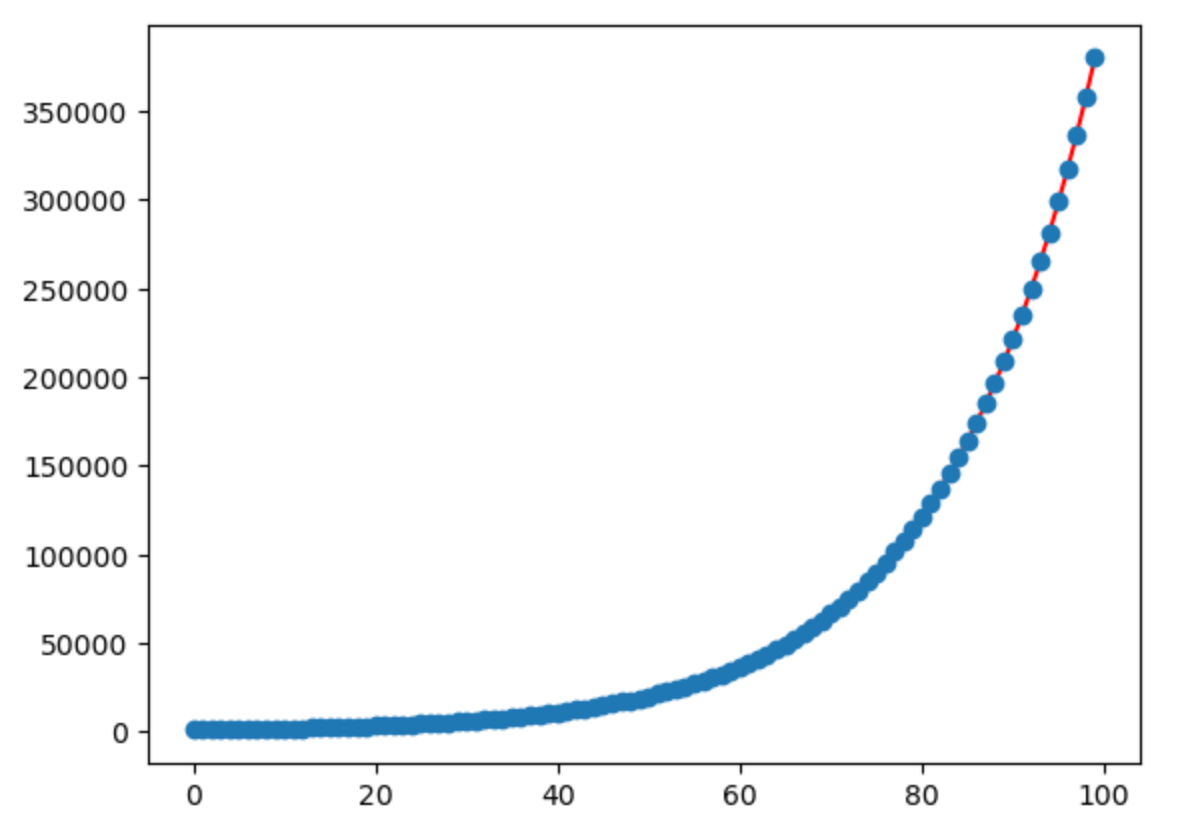
소수점 차이가 약간 날 뿐 거의 동일합니다.
정확한 수치가 필요하지 않다면 자연상수를 이용한 복리법으로 복리가 어떻게 진행되는지나 퀀트 백테스팅시 수익률 계산하는데 보다 쉽게 접근할 수 있을 것 같습니다.
함께보면 좋은글
[미적분] 자연상수 e의 정의
ndarray 데이터로 그래프 그리기(matplotlib)
[matplotlib]여러개로 나누어서 그래프 출력(subplot)
'수학' 카테고리의 다른 글
| 구분구적법 (0) | 2023.08.07 |
|---|---|
| [Python] 파이썬 math모듈 필수 수학함수 정리 (0) | 2023.07.20 |
| [미적분] 자연상수 e의 정의 (0) | 2023.07.13 |
| [파이썬] 사분위수(Quantiles)란? (0) | 2022.11.07 |
| 파이썬으로 정규분포 그리기 (0) | 2022.10.06 |
데이터목장님의
글이 좋았다면 응원을 보내주세요!



