[통계학] 공분산과 상관계수
- 수학
- 2023. 10. 2.
공분산과 상관관계: 데이터 분석의 핵심 개념
데이터 분석 및 통계학 분야에서 중요한 두 가지 개념인 공분산과 상관관계에 대해 알아보겠습니다. 이 개념들은 데이터 간의 관계를 이해하고 해석하는 데 도움을 주는 중요한 역할을 합니다.
1. 공분산 (Covariance)
공분산은 두 변수 간의 관계를 측정하는 지표 중 하나입니다. 두 변수가 어떻게 함께 움직이는지를 보여주는데 사용됩니다. 공분산의 수학적 정의는 다음과 같습니다.
Cov(X,Y)=E[(X−μX)(Y−μY)]
여기서,
- X와 Y는 두 변수,
- Xᵢ와 Yᵢ는 각각의 변수의 개별 데이터 포인트,
- μ_X와 μ_Y는 각각의 변수 X와 Y의 평균,
- n은 데이터 갯수입니다.
정의에서 보듯이 공분산은 X의 편차와 Y의 편차를 곱한것의 평균이라는 뜻이 됩니다.
공분산의 부호는 두 변수 간의 방향성을 나타냅니다.
- 양수 값: 두 변수가 함께 증가하거나 감소하는 경향이 있음을 나타냅니다.
- 음수 값: 하나의 변수가 증가하면 다른 변수는 감소하는 경향이 있음을 나타냅니다.
- 0 값: 두 변수 간의 관계가 없음을 나타냅니다.
사실 정의대로 계산하는 건 너무 힘들기 때문에 간편한 계산을 위해 다음과 같이 쓸 수도 있습니다.
Cov(X,Y) = E(XY)-E(X)E(Y)
실제로 정의를 풀어보면 위의 정리가 되는 걸 확인할 수 있습니다. 다음과 같이 증명을 합니다.
μ_X와 μ_Y를 각각의 변수 X와 Y의 평균이라 할 때,
Cov(X,Y) = E[(X-\mu_X)(Y-\mu_Y)]
= E[XY-\mu_YX-\mu_XY+\mu_X\mu_Y]
= E[XY]-\mu_YE[X]-\mu_XE[Y]+\mu_X\mu_Y
E[X] = \mu_X, E[Y]=\mu_Y 이므로
E[XY]-E[Y]E[X]-E[X]E[Y]+E[X]E[Y] = E[XY]-E[X]E[Y]
사실 공분산의 값 자체로 무언가를 해석하기 어렵습니다. 왜냐하면 X와 Y의 단위 크기에 따라 값이 천지차이가 되기 때문에 불안정합니다.
예를 들어, X,Y가 100점 만점의 시험의 공분산은 최대값과 10점짜리의 시험의 공분산의 최대값의 차이가 많이 날 수 있습니다. 그러면 여러 샘플에서 나오는 값의 상관성을 한눈에 보기가 어렵습니다.
따라서 상관관계를 도입해 값을 안정화시키는 작업을 합니다.
실제로, Cov(X,Y)의 범위를 보면 이해가 됩니다.
t에 대한 다음의 이차함수를 생각해보겠습니다.
g(t) = E[[X-\mu_X]+t(Y-\mu_Y)]^2]
그럼 g(t)\ge0 입니다.
g(t) = t^2E(Y-\mu_Y)^2+2tE[(X-\mu_X)(Y-\mu_Y)]+E[(X-\mu_X)^2]\ge0
g(t)는 t 에 대한 이차함수이므로, 판별식에 의해 다음이 성립합니다.
D/4 = [E[(X-\mu_X)(Y-\mu_Y)]]^2-E[(X-\mu_X)^2]E[(Y-\mu_Y)^2]\le0
따라서,
|E[(X-\mu_X)(Y-\mu_Y)]\le \sqrt{E[(X-\mu_X)^2]} \sqrt{E[(Y-\mu_Y)^2]}
즉,
[Cov(X,Y)]^2 \le \sigma_X^2\sigma_Y^2
이 됩니다.
여기서,
- σ_X는 변수 X의 표준편차,
- σ_Y는 변수 Y의 표준편차입니다.
2. 상관관계 (Correlation)
상관관계는 두 변수 간의 선형 관계의 강도와 방향을 측정하는 지표입니다. 위에서 보인 부등식을 이용하면 상관관계는 -1에서 1 사이의 값을 가지게 될 것입니다. 다음과 같이 정의됩니다.
상관계수(Correlation Coefficient, r) = C(X, Y) / (σ_X * σ_Y)
여기서,
- σ_X는 변수 X의 표준편차,
- σ_Y는 변수 Y의 표준편차입니다.
상관계수의 값이 다음과 같이 해석됩니다.
- 1에 가까운 값: 강한 양의 선형 관계를 나타냅니다.
- -1에 가까운 값: 강한 음의 선형 관계를 나타냅니다.
- 0에 가까운 값: 선형 관계가 없거나 약한 관계를 나타냅니다.
상관계수는 두 변수 간의 관계를 파악하는 데 매우 유용하며, 데이터 분석, 경제학, 과학 연구 등 다양한 분야에서 활용됩니다.
3. 공분산과 상관관계의 활용
공분산과 상관관계는 데이터 분석에서 다음과 같은 용도로 활용됩니다.
- 리스크 관리: 금융 분야에서 주식 가격과 이자율 등과의 관계를 분석하여 리스크를 평가하는 데 사용됩니다.
- 마케팅 전략: 광고 비용과 판매량 간의 관계를 분석하여 마케팅 전략을 개선하는 데 활용됩니다.
- 의학 연구: 약물 복용과 건강 상태 간의 관계를 조사하여 의학 연구에 활용됩니다.
이러한 개념을 이해하고 활용하는 것은 데이터 과학 및 통계 분야에서 중요한 역할을 합니다.
파이썬으로 간단한 예제를 할 수 있는데 가상의 값을 만들어보겠습니다.
import pandas as pd
# 데이터 생성
data = {
'Date': ['2023-01-01', '2023-01-02', '2023-01-03', '2023-01-04', '2023-01-05'],
'Stock_Price': [100.0, 101.5, 102.0, 103.2, 102.8],
'Interest_Rate': [3.0, 2.8, 2.7, 2.9, 3.1]
}
df = pd.DataFrame(data)
# 상관계수 계산
correlation = df['Stock_Price'].corr(df['Interest_Rate'])
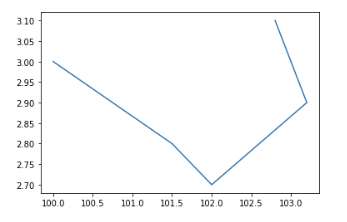
print("주식 가격과 이자율 간의 상관계수:", correlation)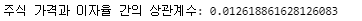
실제로 그림으로 봐도 전혀 관련이 없는듯한 그림으로 나옵니다.
마치며
공분산과 상관관계에 대해서 알아보았는데요. 왜 상관계수를 실제적으로 많이 쓰는 이유를 알게 되는 시간이 되셨으면 좋겠습니다.
'수학' 카테고리의 다른 글
| [미적분] 삼각함수 공식 총정리 (0) | 2023.10.14 |
|---|---|
| [통계학] 상관계수와 회귀계수의 관계 (0) | 2023.10.12 |
| [통계학] 확률의 종류 (0) | 2023.09.04 |
| 구분구적법 (0) | 2023.08.07 |
| [Python] 파이썬 math모듈 필수 수학함수 정리 (0) | 2023.07.20 |
데이터목장님의
글이 좋았다면 응원을 보내주세요!



