물리학과 수학에서의 삼각함수 활용
- 수학
- 2025. 5. 16.
현대 물리학과 수학에서의 삼각함수 활용
삼각함수는 기원전 그리스 시대부터 천문학과 항해에 활용되어 온 수학의 기본 도구입니다. 오늘날 물리학과 수학 분야에서 삼각함수는 단순한 계산 도구를 넘어 자연 현상을 이해하고 설명하는 데 핵심적인 역할을 하고 있습니다. 이 글에서는 현대 물리학과 수학에서 삼각함수가 어떻게 활용되는지 살펴보겠습니다.

물리학에서의 삼각함수 활용
1. 파동 현상 분석
우리 주변의 모든 파동 현상은 삼각함수를 통해 수학적으로 표현됩니다. 음파, 빛, 전자기파, 수면파 등 모든 파동은 기본적으로 사인(sine)과 코사인(cosine) 함수로 모델링됩니다.
파동 방정식의 일반적인 해는 다음과 같이 표현됩니다:
y(x,t)=Asin(kx−ωt+ϕ)
여기서 A는 진폭, k는 파동 수, ω는 각주파수, ϕ는 위상 상수입니다.

2. 진동 운동
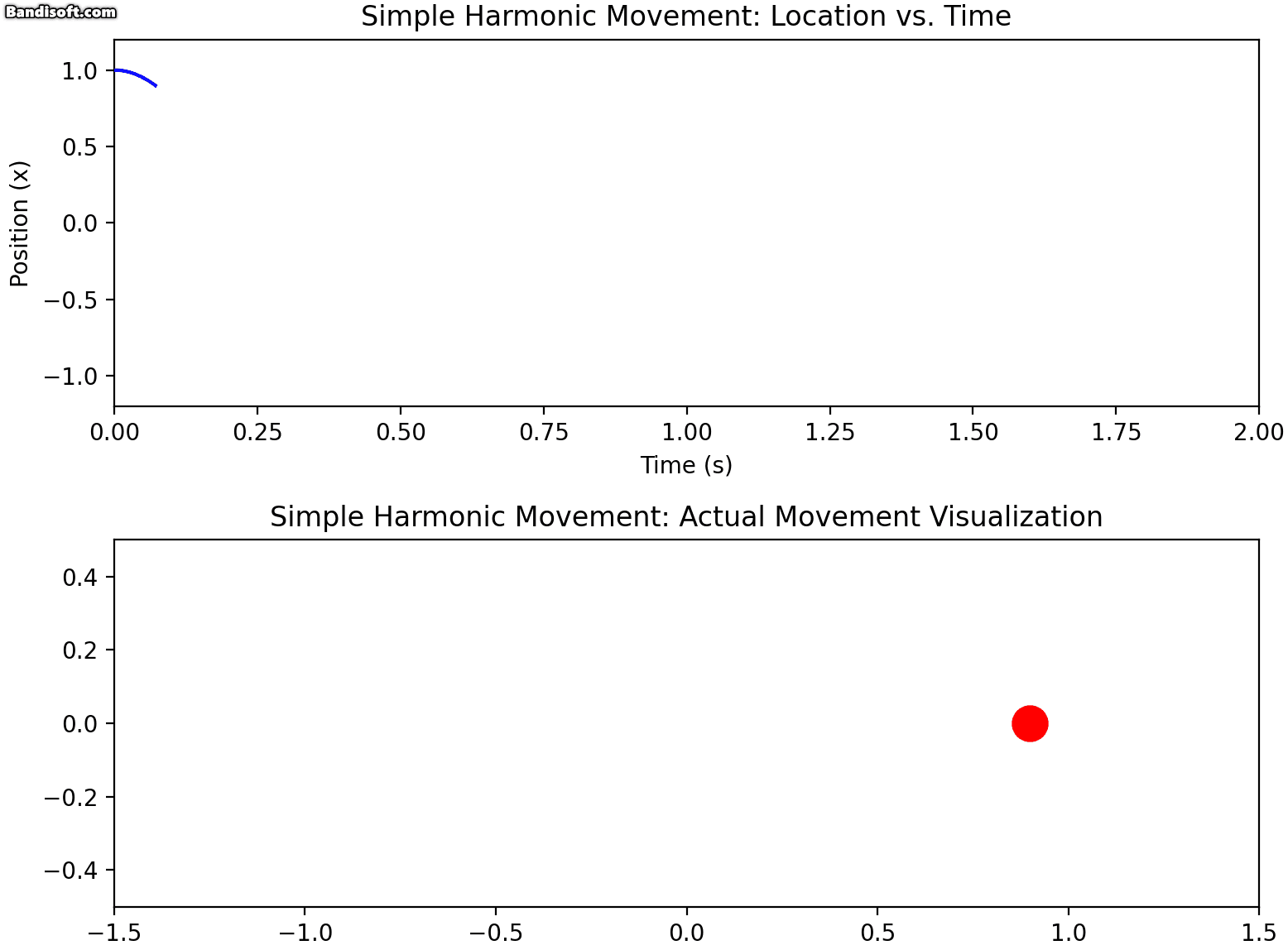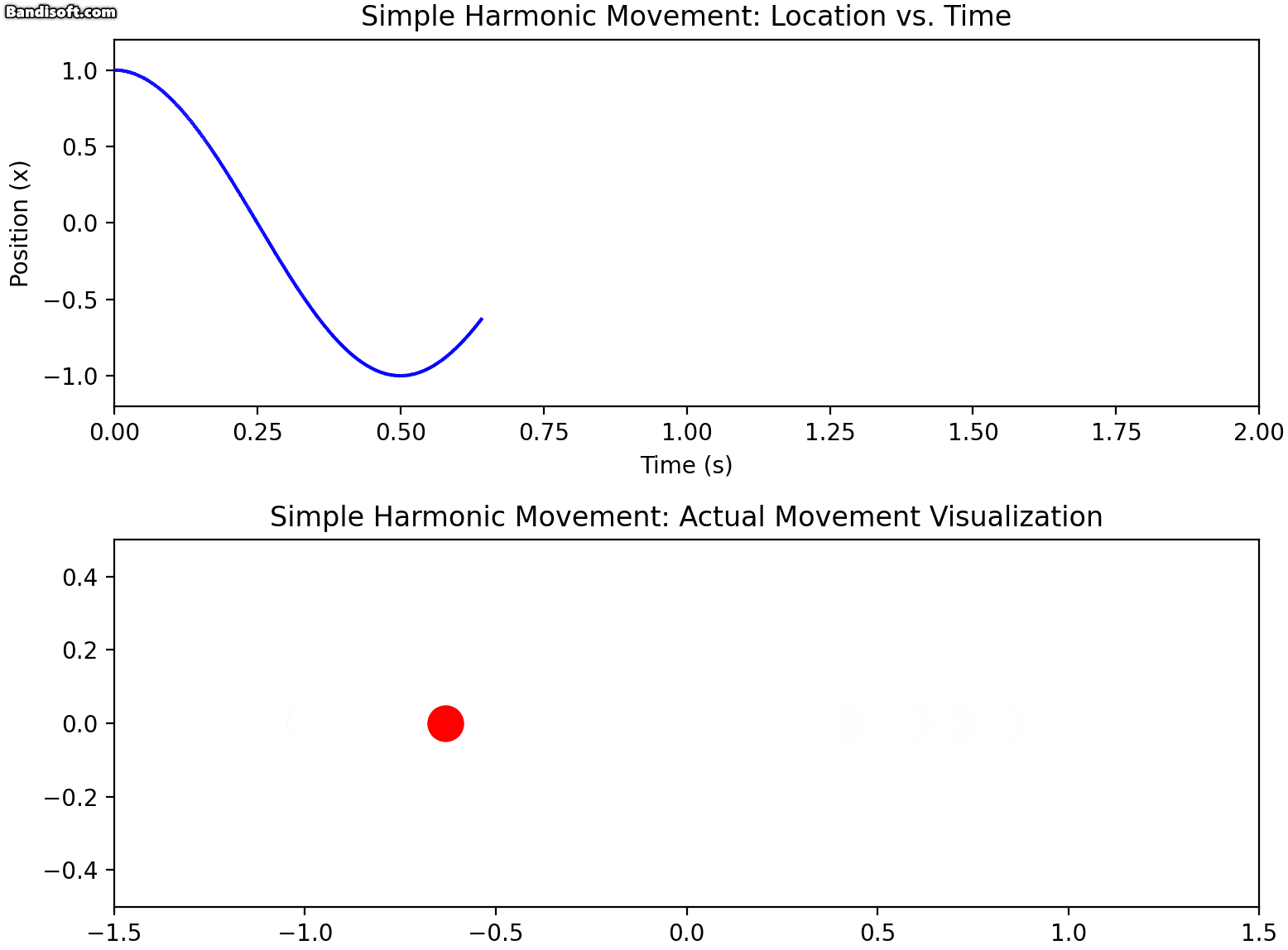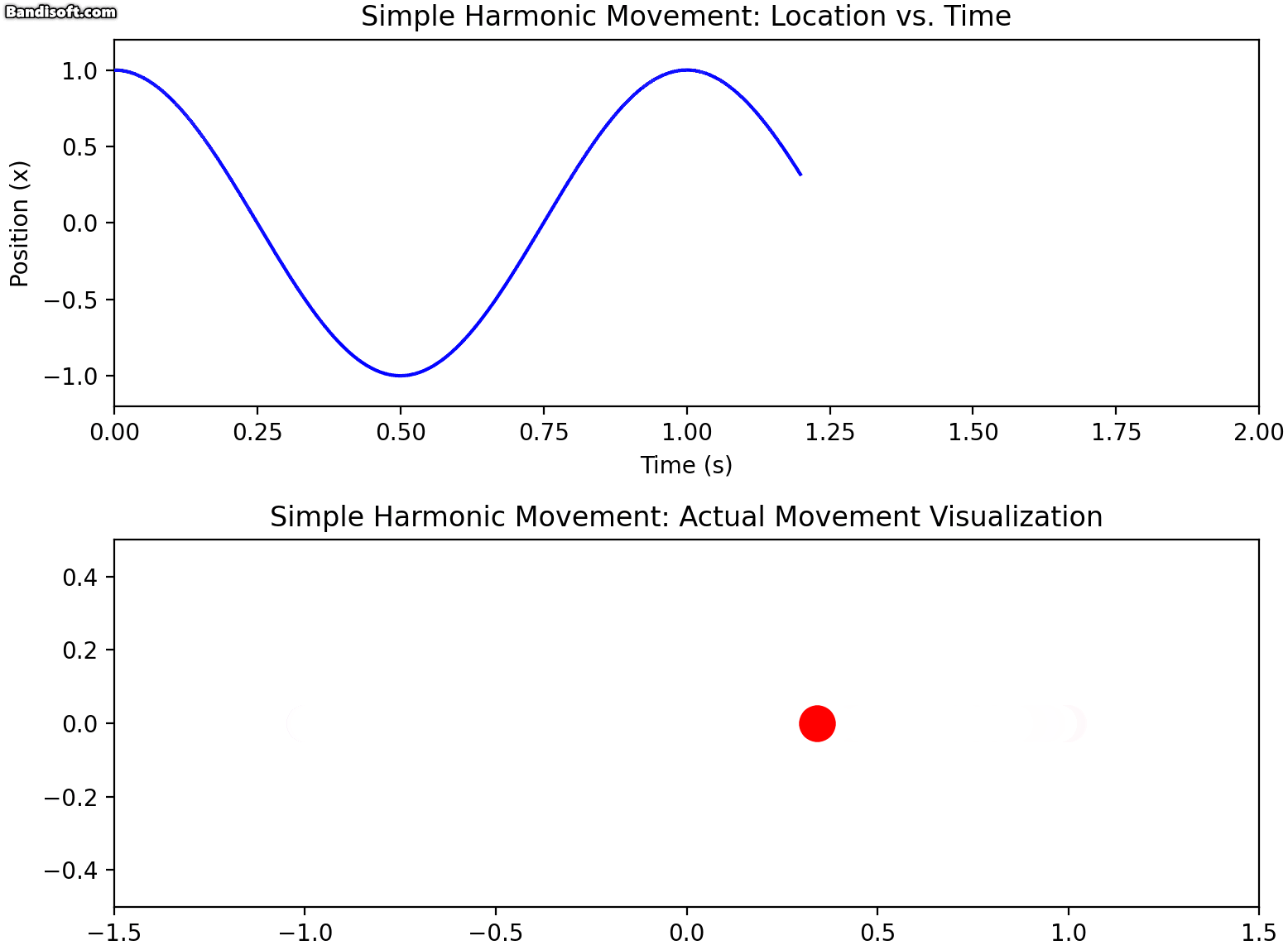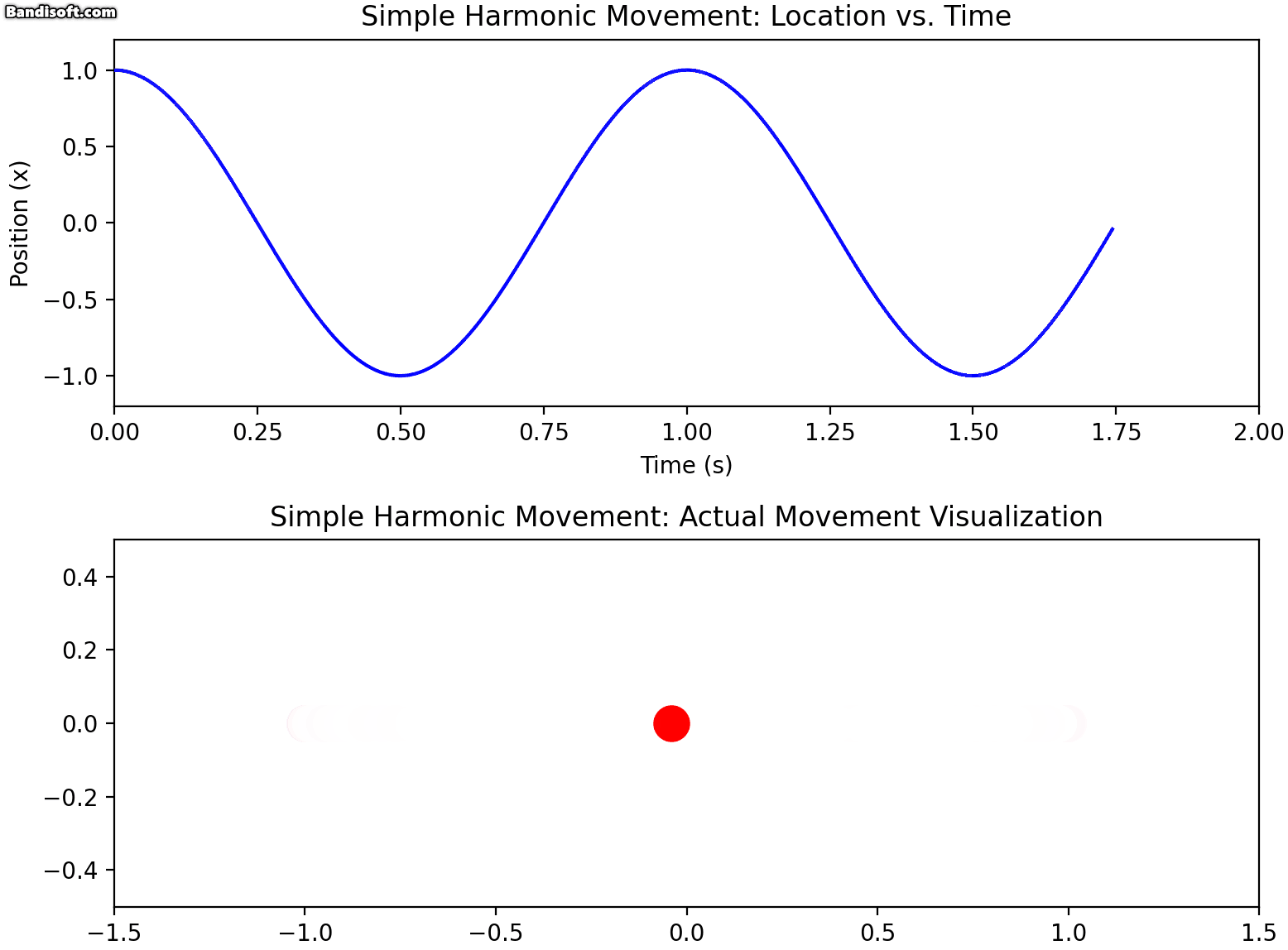
단순 조화 운동(Simple Harmonic Motion)은 물리학에서 가장 기본적인 운동 형태 중 하나입니다. 진자의 움직임, 스프링에 매달린 물체의 진동 등이 대표적인 예입니다.
단순 조화 운동하는 물체의 위치는 시간에 따라 다음과 같이 표현됩니다:
x(t)=Acos(ωt+ϕ)
3. 전자기학
교류 전류와 전압은 시간에 따라 사인 곡선으로 변화합니다. 전자기파의 전기장과 자기장 성분 역시 삼각함수로 표현됩니다.
V(t)=V0sin(ωt)
I(t)=I0sin(ωt+ϕ)
여기서 ϕ는 전압과 전류 사이의 위상차를 나타냅니다.

4. 양자역학
양자역학에서 파동함수의 해는 종종 삼각함수의 형태를 띱니다. 무한 퍼텐셜 우물(infinite potential well) 내 입자의 파동함수는 다음과 같이 표현됩니다: 양자역학에서 가장 기본적인 문제 중 하나로, 고전적으로는 움직일 수 없었던 작은 입자가 특정한 영역 안에서만 존재할 수 있고, 그 밖은 완전히 벽으로 막혀 있는 상황을 말합니다.
ψn(x)=√2Lsin(nπxL)
여기서 L은 우물의 폭이고 n은 양자 수입니다.

5. 상대성 이론
특수 상대성 이론에서 로렌츠 변환과 같은 시공간 좌표 변환에는 삼각함수가 필수적입니다. 속도 v로 움직이는 관성계로의 좌표 변환은 다음과 같이 표현됩니다:
x′=γ(x−vt)
t′=γ(t−vxc2)
여기서 γ=1√1−v2/c2는 로렌츠 인자입니다.

수학에서의 삼각함수 활용
1. 푸리에 해석
복잡한 주기 함수를 사인과 코사인의 무한급수로 분해하는 푸리에 급수는 현대 수학과 공학에서 가장 중요한 도구 중 하나입니다.
f(x)=a02+∑∞n=1[ancos(nx)+bnsin(nx)]
푸리에 변환은 이를 더 확장하여 비주기 함수에도 적용할 수 있게 합니다:
F(ω)=∫∞−∞f(t)e−iωtdt
이는 디지털 신호 처리, 이미지 압축, 차분방정식 해결 등 다양한 분야에 응용됩니다.

2. 미분방정식
많은 미분방정식의 해는 삼각함수를 포함합니다.
예를 들어, 단순 조화 진동자의 운동 방정식: d2xdt2+ω2x=0
의 일반해는 x(t)=Acos(ωt)+Bsin(ωt) 입니다.

3. 복소수 분석
오일러 공식은 삼각함수와 지수함수를 연결하는 아름다운 관계식입니다:
eiθ=cosθ+isinθ
이 공식을 통해 복소수의 극형식 표현과 삼각함수의 덧셈 정리 등을 유도할 수 있습니다.
4. 기하학
삼각법은 각도, 거리, 면적 계산 등 기하학적 문제 해결에 필수적입니다. 코사인 법칙과 사인 법칙은 삼각형의 변과 각의 관계를 규명합니다:
사인 법칙: asinA=bsinB=csinC
코사인 법칙: c2=a2+b2−2abcosC
5. 벡터 분석
벡터의 회전, 내적, 외적 계산에 삼각함수가 사용됩니다. 두 벡터 →a와 →b 사이의 내적은 다음과 같이 표현됩니다:
→a⋅→b=|→a||→b|cosθ
여기서 θ는 두 벡터 사이의 각도입니다.
현대 응용 분야
1. 디지털 신호 처리
오디오, 이미지, 비디오 신호 처리에는 푸리에 변환을 기반으로 한 알고리즘이 광범위하게 사용됩니다. MP3, JPEG, MPEG 등의 압축 기술은 모두 삼각함수를 이용한 푸리에 해석에 기반합니다.
2. 컴퓨터 그래픽스
3D 모델링, 애니메이션, 게임 개발에서 물체의 회전과 이동에 삼각함수가 사용됩니다. 회전 행렬은 다음과 같이 표현됩니다:
Rz(θ)=(cosθ−sinθ0 sinθcosθ0 001)
3. 의료 영상
CT, MRI 등의 의료 영상 기술은 라돈 변환과 역변환을 사용하며, 이는 푸리에 변환과 밀접하게 관련되어 있습니다.
4. 통신 시스템
디지털 통신에서 변조 및 복조 기술(AM, FM, PM)은 삼각함수에 기반합니다. 또한 안테나 설계와 전파 패턴 분석에도 삼각함수가 활용됩니다.
5. 제어 이론
자동차의 서스펜션 시스템, 로봇의 제어 등 진동을 다루는 모든 제어 시스템에서 삼각함수를 활용한 모델링이 필수적입니다.
자동차가 범프를 지날 때, 서스펜션 시스템은 승차감을 유지하기 위해 진동을 흡수해야 합니다. 도로의 불규칙한 표면은 종종 다양한 주파수의 사인파 조합으로 근사할 수 있습니다. 이는 푸리에 급수의 원리를 이용한 것으로, 복잡한 주기 함수를 여러 사인파와 코사인파의 합으로 표현합니다.
마무리
삼각함수는 단순한 수학적 도구를 넘어 자연 현상을 이해하고 모델링하는 데 필수적인 언어입니다. 물리학, 공학, 의학, 컴퓨터 과학 등 다양한 분야에서 삼각함수는 복잡한 현상을 설명하고 예측하는 데 중요한 역할을 합니다. 디지털 시대에도 삼각함수의 중요성은 계속해서 확대되고 있으며, 삼각함수에 대한 깊은 이해는 현대 과학기술을 이해하는 데 있어 필수적인 요소라고 할 수 있습니다.
참고 문헌
- Boas, M. L. (2006). Mathematical Methods in the Physical Sciences. Wiley.
- Feynman, R. P., Leighton, R. B., & Sands, M. (2011). The Feynman Lectures on Physics. Basic Books.
- Kreyszig, E. (2011). Advanced Engineering Mathematics. Wiley.
- Arfken, G. B., Weber, H. J., & Harris, F. E. (2013). Mathematical Methods for Physicists. Academic Press.
- Oppenheim, A. V., & Willsky, A. S. (1997). Signals and Systems. Prentice Hall.
- Brigham, E. O. (1988). The Fast Fourier Transform and Its Applications. Prentice Hall.
- Bracewell, R. N. (2000). The Fourier Transform and Its Applications. McGraw-Hill.
- Strang, G. (2019). Linear Algebra and Learning from Data. Wellesley-Cambridge Press.
- MathWorld - Wolfram Research: http://mathworld.wolfram.com/
- Paul's Online Math Notes: http://tutorial.math.lamar.edu/
- MIT OpenCourseWare - Physics: https://ocw.mit.edu/courses/physics/
- Khan Academy - Trigonometry: https://www.khanacademy.org/math/trigonometry
함께 보면 좋은 글
삼각함수 기본 개념
** '삼각함수'하면 어떤 이미지가 떠오르시나요?**복잡한 공식, 꼬불꼬불한 그래프, 끝없이 이어지는 계산... 아마 많은 분들이 삼각함수를 '수학의 벽'이라고 생각하실지도 모르겠습니다. 중학교
seong6496.tistory.com
고대에도 삼각비를 사용했다고? 고대 삼각비의 역사
고대에도 삼각비를 사용했다고? 고대 삼각비의 역사삼각비는 우리가 수학 시간에 익숙하게 배우는 개념 중 하나입니다. 보통 직각삼각형에서 각도와 변의 길이 사이의 관계를 다룰 때 쓰이죠.
seong6496.tistory.com
'수학' 카테고리의 다른 글
| 피타고라스와 삼각함수의 연결고리 (2) | 2025.05.18 |
|---|---|
| 삼각함수 특수각 암기법 (2) | 2025.05.17 |
| 고대에도 삼각비를 사용했다고? 고대 삼각비의 역사 (2) | 2025.05.15 |
| 삼각함수 기본 개념 (1) | 2025.05.13 |
| 이산수학 RSA 암호 (1) | 2025.05.13 |



