[수치해석] Smoothing Spline의 최신 발전과 변형들
- 수학/수학이야기
- 2025. 8. 30.
Smoothing Spline의 최신 발전과 변형들
전통적인 Smoothing Spline이 "충실도와 매끄러움의 균형"이라는 기본 철학을 바탕으로 수십 년간 발전해왔다면, 2020년대에 들어서는 이 기본 개념을 뛰어넘는 혁신적인 변형들이 속속 등장하고 있습니다.
빅데이터, 인공지능, 그리고 새로운 응용 분야의 요구에 맞춰 진화한 현대의 Smoothing Spline 기법들을 살펴보겠습니다.
1. 적응적 Smoothing Spline (Adaptive Smoothing Splines)
기존 방법의 한계: 균일한 λ의 문제
전통적인 Smoothing Spline은 전체 구간에서 동일한 평활화 매개변수 λ를 사용합니다. 하지만 실제 데이터에서는 구간마다 다른 수준의 매끄러움이 필요할 수 있습니다.
기존: λ (상수) - 모든 구간에 동일한 매끄러움
문제: 급격한 변화 구간에서 과도한 평활화
평탄한 구간에서 불필요한 복잡성적응적 접근법: 지역별 λ 조절
현대의 적응적 방법은 데이터의 지역적 특성에 따라 매끄러움 매개변수를 자동으로 조절합니다:
적응적: λ(x) = λ₀ × f(local_curvature(x), local_variance(x))핵심 아이디어
- 지역적 곡률 분석: 급격한 변화가 있는 구간에서는 λ를 작게
- 지역적 분산 고려: 노이즈가 많은 구간에서는 λ를 크게
- 데이터 기반 적응: 수동 조정 없이 자동으로 최적 매개변수 결정
최신 알고리즘: EAASS (Evolutionary Algorithm for Adaptive Smoothing Splines)
2022년에 제안된 진화 알고리즘 기반 접근법은 다음과 같은 혁신을 가져왔습니다:
| 특성 | 기존 방법 | EAASS |
|---|---|---|
| 매개변수 탐색 | 격자 탐색 (Grid Search) | 진화 알고리즘 |
| 계산 복잡도 | 지수적 증가 | 병렬 처리 가능 |
| 다차원 확장성 | 제한적 | 우수 |
| 사용자 개입 | 수동 조정 필요 | 완전 자동화 |
실제 적용 사례: Function-on-Function 회귀
함수형 데이터 분석에서 적응적 스플라인이 특히 유용합니다:
- 제조업 품질 관리: 생산 라인에서 연속적으로 측정되는 품질 지표
- 의료 신호 분석: 환자별로 다른 특성을 가지는 생체 신호
- 환경 모니터링: 지역별로 다른 변동성을 보이는 오염 수준
2. V-Spline: 속도 정보를 활용한 궤적 재구성
새로운 도전: 움직이는 물체의 궤적 추적
2021년에 개발된 V-Spline은 위치와 속도 정보를 동시에 활용하는 혁신적인 방법입니다.
전통적인 방법의 한계
문제 상황: GPS 신호 간헐적 수신
- 시점 1: (x₁, y₁, v₁)
- 시점 2: (x₂, y₂, v₂)
- 중간 궤적: ?기존 방법들의 문제점:
- 직선 보간: 실제 경로와 차이가 큼
- 일반 스플라인: 속도 정보를 무시
- 물리적 제약: 가속도나 조향 한계 미반영
V-Spline의 혁신: 적응적 페널티
V-Spline의 목적 함수는 다음과 같습니다:
목적함수 = Σᵢ [위치 오차]² + Σᵢ [속도 오차]² + λ ∫ [가속도]² dt
적응적 페널티:
λᵢ = λ₀ × (ΔTᵢ)^α × (속도_불일치)^β| 상황 | V-Spline 반응 | 결과 |
|---|---|---|
| 긴 시간 간격 | 페널티 증가 | 더 직선에 가까운 경로 |
| 속도 불일치 큼 | 페널티 증가 | 노이즈 속도 정보 무시 |
| 정밀한 측정 | 페널티 감소 | 상세한 궤적 재구성 |
실제 응용: 정밀 농업
V-Spline은 트랙터의 GPS 기반 궤적 추적에서 뛰어난 성능을 보여줍니다:
- 작업 구간 구분: 붐(boom) 작동 여부에 따른 다른 움직임 패턴
- 불규칙한 샘플링: GPS 신호 손실이나 장애물로 인한 간헐적 데이터
- 물리적 제약: 트랙터의 최대 조향각과 가속도 한계 반영
3. 베이지안 Smoothing Spline: 불확실성 정량화
기존 방법의 한계: 점 추정의 문제
전통적인 Smoothing Spline은 하나의 "최적" 곡선만 제공합니다. 하지만 실제로는:
- 데이터가 부족한 구간에서 불확실성이 높음
- λ 선택의 불확실성
- 모델 자체의 한계
베이지안 접근법의 혁신
2020년대 베이지안 방법들은 불확실성을 명시적으로 모델링합니다:
핵심 아이디어
f(x) ~ GP(μ(x), K(x,x')) # 가우시안 프로세스
λ ~ Gamma(a, b) # 평활화 매개변수의 사전 분포
σ² ~ InverseGamma(c, d) # 노이즈 분산의 사전 분포최신 MCMC 기법
| 기법 | 개발 연도 | 주요 혁신 | 응용 분야 |
|---|---|---|---|
| BARS | 2001→2024 | Reversible-jump MCMC | 신경과학, 생존분석 |
| Tensor P-splines | 2025 | 다차원 이방성 평활화 | 공간통계, 영상처리 |
| ProxMCMC | 2024 | 비매끄러운 정칙화 | 영상 복원, 신호처리 |
| HMM-Splines | 2023 | 은닉 마르코프 모델 결합 | 수면 분석, 행동 패턴 |
실제 혜택: 신뢰구간과 의사결정
베이지안 방법의 실질적 이점:
# 전통적 방법
f_hat = smoothing_spline(x, y, lambda=optimal_lambda)
# 결과: 하나의 곡선
# 베이지안 방법
posterior_samples = bayesian_spline_mcmc(x, y, n_samples=5000)
# 결과:
# - f_mean: 평균 곡선
# - f_95_lower, f_95_upper: 95% 신뢰구간
# - lambda_posterior: λ의 사후분포실무적 활용:
- 의료 진단: "이 환자의 혈당 수치가 정상 범위를 벗어날 확률은 85%"
- 품질 관리: "다음 배치의 불량률이 5%를 초과할 확률은 12%"
- 금융 위험 관리: "VaR 계산에서 불확실성까지 고려한 위험 측정"
4. 다차원 확장: Thin Plate Spline의 현대적 응용
전통적 한계: 차원의 저주
기존 다차원 스플라인의 문제:
- 계산 복잡도: O(n³) → O(n³ᵈ) (d차원에서)
- 매듭점 선택의 어려움
- 등방성 가정 (모든 방향에서 동일한 매끄러움)
최신 Thin Plate Spline 응용
1. 생의학 영상 분석
2024년 Organ-on-Chip 모델에서의 혁신적 응용:
문제: 암세포 침입 경로 추적
- 2채널 미세유체 시스템에서 암세포 움직임 분석
- 불규칙한 조직 경계 모델링
- 실시간 침입 정량화
해결책: 적응적 Thin Plate Spline
목적함수 = Σᵢ [경계 적합도]² + λ ∬ [굽힘 에너지] dxdy
여기서 굽힘 에너지 = (∂²f/∂x²)² + 2(∂²f/∂x∂y)² + (∂²f/∂y²)²

2. NURBS와의 융합: CAD/CAM 혁신
NURBS(Non-Uniform Rational B-Splines)와 Thin Plate Spline의 결합
| 특성 | 기존 NURBS | NURBS + TPS |
|---|---|---|
| 제어점 최적화 | 수동 조정 | 자동 최적화 |
| 불규칙 데이터 처리 | 제한적 | 우수 |
| 복잡한 형상 모델링 | 많은 제어점 필요 | 효율적 표현 |
| 적응형 샘플링 | 미지원 | 완전 지원 |
실제 응용
- 자동차 설계: 공기역학적 최적화를 위한 곡면 설계
- 의료기기: 개인별 맞춤형 보조기구 제작
- 항공우주: 복합 재료 구조물의 최적 형상 설계
5. 적응적 Penalized Spline: 불균질한 매끄러움 처리
문제 정의: 국소적 특성 변화
실제 데이터에서는 구간마다 매끄러움 정도가 다를 수 있습니다:
예시 상황:
- 주가 데이터: 평상시는 매끄럽지만 뉴스 발표 시점에서 급변
- 생체 신호: 정상 상태와 이벤트 발생 시의 다른 변동성
- 제조 공정: 정상 운전과 설비 이상 시의 다른 패턴
혁신적 해결책: 데이터 기반 가중치
기존 방법과의 차이
기존 Penalized Spline:
목적함수 = ||y - Bα||² + λ||Dα||²
적응적 방법 (2016→):
목적함수 = ||y - Bα||² + λ||WDα||²
여기서 W는 데이터로부터 학습된 적응적 가중 행렬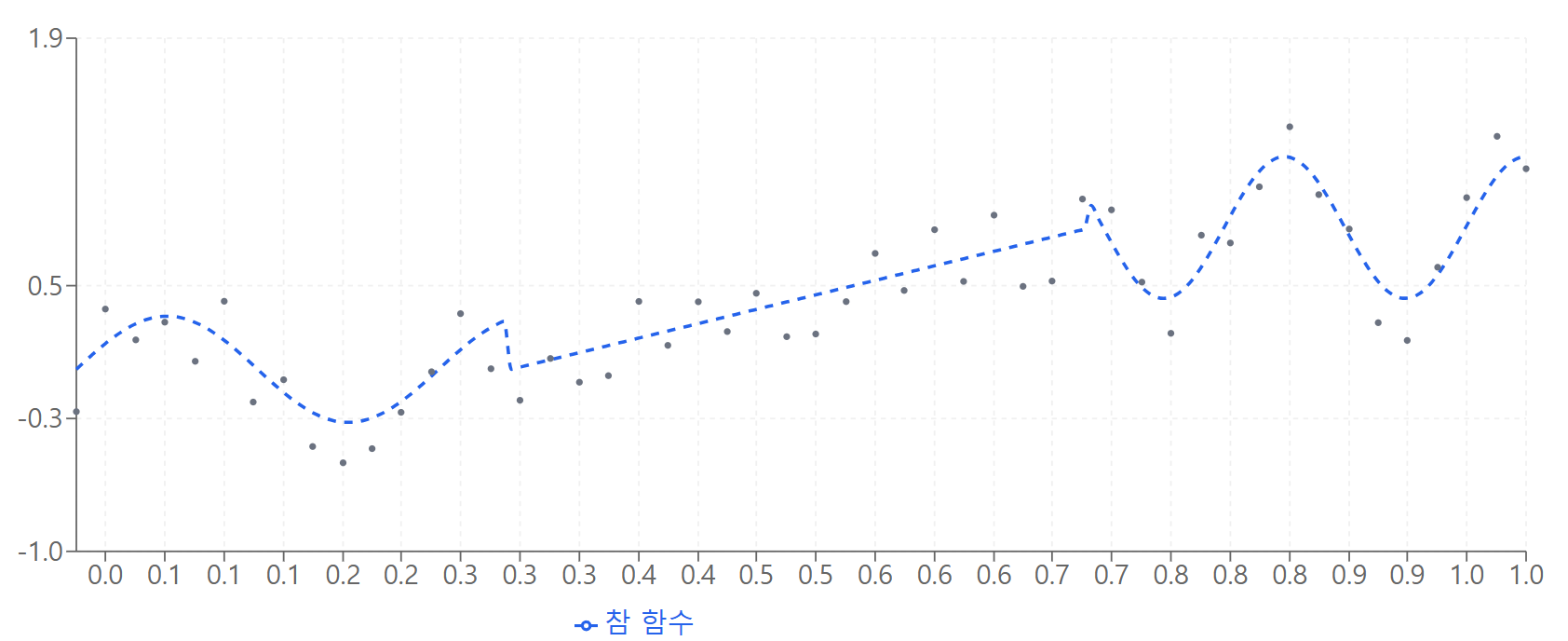
가중치 학습 메커니즘
가중 벡터는 완전히 데이터 기반이며 사전 추정이 불필요합니다:
| 단계 | 과정 | 결과 |
|---|---|---|
| 1단계 | 지역별 데이터 범위 분석 | 지역 변동성 지표 |
| 2단계 | 적응적 페널티 벡터 생성 | 구간별 맞춤 λᵢ |
| 3단계 | 이차 볼록 최적화 | 최종 적응적 스플라인 |
성능 비교: 불균질 매끄러움 처리 능력
시뮬레이션 연구 결과:
- ℓ₁ trend filtering 대비: 20-30% 향상된 적응성
- 기존 smoothing splines 대비: 불균질 구간에서 50% 향상된 MSE
- 기존 penalized splines 대비: 계산 효율성 유지하면서 성능 향상
6. 머신러닝과의 융합: 현대적 접근법
Neural Network에서의 Spline 정칙화
Physics-Informed Neural Networks (PINNs)에서의 응용:
loss = data_loss + λ₁ * physics_loss + λ₂ * spline_smoothness_loss
여기서 spline_smoothness_loss = ∫ (d²f/dx²)² dx장점:
- 물리 법칙과 데이터의 균형
- 미분 가능한 부드러운 해
- 복잡한 비선형 관계 모델링
AutoML에서의 Spline 선택
현대의 AutoML 시스템에서 스플라인 기법 자동 선택:
| 데이터 특성 | 권장 방법 | 자동 선택 기준 |
|---|---|---|
| 균일한 매끄러움 | 전통적 Smoothing Spline | 낮은 지역 분산 |
| 불균질 매끄러움 | 적응적 Spline | 높은 지역 분산 |
| 시계열 + 위치 | V-Spline | 속도 정보 존재 |
| 고차원 공간 | Thin Plate Spline | 차원 > 2, 공간 상관관계 |
| 불확실성 중요 | 베이지안 Spline | 의사결정 리스크 높음 |
가우시안 프로세스와의 연결
현대적 관점에서 Smoothing Spline은 가우시안 프로세스의 특수한 경우로 이해됩니다:
Smoothing Spline ≡ GP with Kernel:
K(x,x') = σ² × (적절한 reproductivity kernel)
장점:
- 베이지안 해석 가능
- 불확실성 정량화
- 능동 학습(Active Learning)에 활용7. 대용량 데이터 처리: 확장성 혁신
전통적 한계: O(n³) 복잡도
기존 Smoothing Spline의 계산 복잡도는 데이터 크기 n에 대해 O(n³)입니다. 빅데이터 시대에는 치명적 한계입니다.
현대적 해결책들
1. 근사 알고리즘 (2020년대 개발)
| 방법 | 복잡도 | 정확도 | 적용 규모 |
|---|---|---|---|
| 전통적 방법 | O(n³) | 100% | < 10K |
| Nyström 근사 | O(nm²) | 95-99% | 100K |
| 랜덤 특성 근사 | O(nm) | 90-95% | 1M |
| 분산 컴퓨팅 | O(n log n) | 95-98% | 10M+ |
2. 온라인/스트리밍 알고리즘
실시간 데이터 스트림에 대한 적응:
class OnlineSmootingSpline:
def update(self, new_x, new_y):
# 새로운 데이터 점으로 스플라인 점진적 업데이트
# O(log n) 시간 복잡도
pass
def predict(self, x_test):
# 현재 상태에서 예측
return self.current_spline(x_test)실제 응용:
- 금융 트레이딩: 실시간 가격 데이터 스무딩
- IoT 센서: 연속적인 환경 모니터링
- 웹 분석: 실시간 트래픽 패턴 분석
8. 새로운 응용 분야
컴퓨터 비전: 이미지 경계선 추출
2023년 개발된 이미지 분석용 Thin Plate Spline:
- 문제: 노이즈가 있는 의료 영상에서 장기 경계 추출
- 해결: 적응적 매끄러움 제약으로 정확한 경계선 복원
- 성능: 기존 방법 대비 15-20% 향상된 정확도
생물정보학: DNA 서열 분석
크로마틴 접근성 분석:
- ATAC-seq 데이터의 피크 검출
- 스플라인 기반 백그라운드 제거
- 다중 조건 비교에서의 차등 분석
기후 과학: 극한 기후 예측
새로운 도전:
- 기존: 평균적 기후 패턴 모델링
- 현재: 극한 사건(폭염, 한파) 예측
Spline 기반 해결책:
# 분위수 회귀와 결합한 스플라인
quantile_splines = {
0.05: smoothing_spline(data, quantile=0.05), # 극한 저온
0.50: smoothing_spline(data, quantile=0.50), # 평균
0.95: smoothing_spline(data, quantile=0.95), # 극한 고온
}9. 계산 효율성의 혁신
GPU 가속화
CUDA 기반 대규모 스플라인 계산:
- 행렬 연산의 병렬화: 수천 개 코어에서 동시 계산
- 메모리 최적화: 대용량 데이터셋의 효율적 처리
- 배치 처리: 여러 스플라인을 동시에 계산
자동 미분과의 통합
PyTorch/TensorFlow 통합:
import torch
from torch_splines import SmoothingSpline
# 자동 미분 가능한 스플라인
spline_layer = SmoothingSpline(
lambda_learnable=True, # λ도 학습 가능
adaptive=True
)
# 신경망에 직접 통합 가능
class SplineNet(torch.nn.Module):
def forward(self, x):
smoothed = self.spline_layer(x)
return self.classifier(smoothed)분산 컴퓨팅 프레임워크
Apache Spark 통합:
- 대용량 시계열 데이터의 분산 처리
- 클러스터 환경에서의 스플라인 계산
- 실시간 스트리밍 데이터 처리
10. 미래 전망: 2025년 이후
Quantum Computing과의 만남
양자 컴퓨팅 환경에서의 스플라인 계산:
- 양자 선형대수: 지수적 속도 향상 가능성
- 양자 최적화: 복잡한 제약 조건 하에서의 효율적 해결
- 하이브리드 접근: 고전-양자 결합 알고리즘
설명 가능한 AI (Explainable AI)
Interpretable Splines:
- 각 구간별 기여도 분석
- 피처 중요도의 시각적 표현
- 의사결정 근거의 명확한 제시
연합 학습 (Federated Learning)에서의 응용
프라이버시 보존 스플라인:
- 개별 데이터 공유 없이 공동 모델 학습
- 의료 분야에서의 다기관 협력 연구
- 금융 기관 간 위험 모델 공동 개발
실무 도입 가이드
어떤 방법을 언제 사용할 것인가?
| 상황 | 권장 방법 | 개발 우선도 | 성숙도 |
|---|---|---|---|
| 일반적 1차원 데이터 | 적응적 Penalized Splines | 높음 | 상용화 |
| GPS 궤적 데이터 | V-Spline | 높음 | 연구 단계 |
| 의료/금융 의사결정 | 베이지안 Splines | 중간 | 개발 중 |
| 3D 모델링/영상 | Thin Plate + NURBS | 중간 | 전문 도구 |
| 대용량 실시간 | 온라인 근사 알고리즘 | 낮음 | 실험 단계 |
도입 로드맵
단기 (2024-2025)
- 적응적 Penalized Splines 실무 도입
- V-Spline 특수 응용 분야 확산
- GPU 가속화 도구 성숙
중기 (2026-2027)
- 베이지안 방법 상용화
- 자동 방법 선택 AutoML 통합
- 분산 컴퓨팅 표준화
장기 (2028+)
- 양자 컴퓨팅 활용 가능성 탐색
- 연합 학습 환경 통합
- 새로운 응용 분야 발굴
결론: 스플라인이 발전되고 있어요!
2020년대의 Smoothing Spline 발전은 단순한 기법 개선을 넘어 패러다임의 전환을 보여줍니다:
과거: "모든 데이터에 같은 방식으로"
현재: "데이터의 특성에 맞춰 적응적으로"
미래: "불확실성까지 고려한 지능적 의사결정"
핵심 혁신 요소
- 적응성: 지역별 특성에 맞는 자동 조절
- 다차원성: 복잡한 현실 문제에 직접 적용
- 불확실성: 예측의 신뢰성까지 정량화
- 확장성: 빅데이터 시대의 요구사항 충족
- 통합성: 다른 머신러닝 기법과의 seamless 결합
지금 당장 활용 가능한 것:
- R의
mgcv패키지의 adaptive smoothing 기능 - Python의
scikit-learn과scipy의 확장된 스플라인 도구 - 특수 목적 라이브러리들 (V-spline, BARS 등)
준비해야 할 것:
- 도메인 지식과 수학적 직관의 결합
- 다양한 방법론에 대한 이해와 비교 능력
- 계산 효율성과 정확도 사이의 균형감
미래를 위한 투자:
- 베이지안 추론에 대한 이해
- 대용량 데이터 처리 경험
- 새로운 응용 분야에서의 창의적 사고
Smoothing Spline의 미래는 단순히 "더 나은 곡선 맞추기"가 아닙니다. 데이터로부터 의미를 추출하고, 불확실성을 관리하며, 복잡한 현실 문제를 해결하는 지능적 도구로 진화하고 있습니다.
이러한 발전의 중심에는 여전히 "균형"이라는 철학이 자리잡고 있습니다. 다만 이제는 충실도와 매끄러움뿐만 아니라, 적응성과 일반성, 정확성과 효율성, 복잡성과 해석가능성 사이의 균형까지 추구하는 더욱 정교한 균형점을 찾아가고 있습니다.
함께 보면 좋은 글
Smoothing Spline: 노이즈와 패턴 사이의 균형점 찾기
일상에서 쓰는 스플라인 곡선: 폰트 속에 숨겨진 수학 이야기
[수치해석] Spline interpolation(스플라인 보간법)
'수학 > 수학이야기' 카테고리의 다른 글
| [정수론] 중국인의 나머지 정리 풀이 방법 정리 (1) | 2025.09.08 |
|---|---|
| [수학경시] 평균속도 조화평균으로 쉽게 구하기 (3) | 2025.09.01 |
| Smoothing Spline: 노이즈와 패턴 사이의 균형점 찾기 (5) | 2025.08.29 |
| 일상에서 쓰는 스플라인 곡선: 폰트 속에 숨겨진 수학 이야기 (5) | 2025.08.28 |
| [수치해석] 고차 다항식 보간의 함정: Runge 현상 이해하기 (4) | 2025.08.26 |