[Python] 회귀(Regression)
- 데이터 사이언스 / 머신러닝 딮러닝
- 2021. 10. 30.
회귀 분석을 파이썬으로 구현(?)해보겠습니다.
회귀분석을 통해서 데이터 분석을 많이 하게 되는데요.
보통 선형 회귀 모델을 많이 쓰고 있는데
이번 포스팅에서는 일반적인 모형을 통해 전체적인 메커니즘을 정리해볼까 합니다.
오차에 대한 얘기는 빼겠습니다.
추후에 오차체크종류나 선형 회귀나 로지스틱 회귀에 대해 포스팅하겠습니다. 기회가 있다면요 ㅎㅎ
회귀 분석
회귀 분석이란 어떤 실험에 의해서 모여진 데이터(x,y 변수)에 대해 두 변수 사이의 모형을 구해 적합도를 측정하는 것이라 볼 수 있습니다.
x에 따라 y값을 정할 수 있는 경우에 회귀분석을 쓰고 이런 관계에서 x는 독립변수, y는 종속변수라고 합니다.
적합한 모형의 선택은 분석자의 판단에 따라 달라지고 그에 따른 결과 또한 달라지게 됩니다.
회귀 분석을 하는 이유는 독립변수에 따른 종속변수 관계를 이해할 수 있고 일관성 있고 정확성이 높은 모형일수록 종속변수를 예측이 가능해집니다. 데이터를 통해 표준화된 모형을 만든다고 이해하시면 될 것 같습니다.
거꾸로 안정적인 표준화 모형이 있다면 이 모형과 비슷하게 움직이는 데이터에 적용해 빠른 분석과 상관도를 기대할 수도 있습니다.
수학적으로 표현하면 다음과 같습니다.
수학적 문제로 본다면 최소제곱 방법이 기반인데 더 일반화된 상황이라 보시면 될것같습니다.
목표는 만든 모형이 주어진 데이터의 분포를 최대한 내포하면서 데이터의 경향을 한눈에 보게 할 수 있게 하는것입니다.
데이터와 만든 모형간의 오차가 최소화 되게끔 해야하는게 가장 큰 문제이기도 합니다.
그래서 적당한 파라미터를 곱하면서 오차를 최소화하는 방식으로 접근합니다.
수식으로 나타내면 다음과 같습니다.
데이터 셋 {(xi,yi)}, i=1,...,I 와 기저함수 bd, d=1,...,D 에 대하여,
오차를 최소화할 파라미터 α1,α2,...,αD 를 찾기 위해서는 다음의 식의 값을 찾아야 합니다.
min
최소제곱 방법의 일반화된 식이라 생각할 수 있는데 최소 제곱방법에서 직선으로 근사시킬 때 y= a+bx 로 놓고 시작하는데 이를 위 식에 비춰보면 기저함수를 1, x 로 놓았을 때의 계수를 찾아가는 방법이 됩니다.
따라서 내가 정할 모형에 따라 기저함수(곡선의형태) 를 마음대로 정할 수 있고 그에 맞는 파라미터를 찾아가면 됩니다.
파이썬으로 구현
기저함수를 b_1 = 1, b_2 = x, b_3 = x^2,... 로 설정하면 polynomial 형태가 됩니다.
그러면 각 차수의 계수를 구하면 되는 문제가 됩니다. 물론 차수를 얼마나 할지는 스스로 정해야합니다.
이전 포스팅에서 보간법으로 다루었던 f(x)를 그대로 가져와서 해보겠습니다.
f(x) = sinx + 0.5x 입니다. sin 함수가 급수로 표현 가능하기 때문에 polynomial로 접근한다면
비교적 정확할 것이라 생각할 수 있습니다. 정말로 그런지 해보겠습니다.
np.polyfit() 메쏘드로 polynomial을 만들 수 있어서 간단하게 할 수 있습니다.
값을 가져오려면 np.polyval()를 이용하면 됩니다.
먼저 np.polyfit()을 이용해 직선(1차식)으로 표현해 회귀를 해보겠습니다.
import numpy as np
from pylab import plt,mpl
#그래프 모눈종이처럼 보이게 하기
plt.style.use('seaborn')
mpl.rcParams['font.family']='serif'
%matplotlib inline
# 셋팅
def f(x):
return np.sin(x)+0.5*x
def create_plot(x,y, styles, labels, axlabels):
plt.figure(figsize=(10,5))
for i in range(len(x)):
plt.plot(x[i],y[i],styles[i],label=labels[i])
plt.xlabel(axlabels[0])
plt.ylabel(axlabels[1])
plt.legend(loc=0)
x = np.linspace(-2*np.pi,2*np.pi,25)
# 1차식(직선의 최소제곱방법)
res = np.polyfit(x,f(x),deg=1, full=True)
# 비교를 위해 값 추출
y = np.polyval(res[0],x)
create_plot([x,x],[f(x),y],['b','ro'],['f(x)','regression'],['x','f(x)'])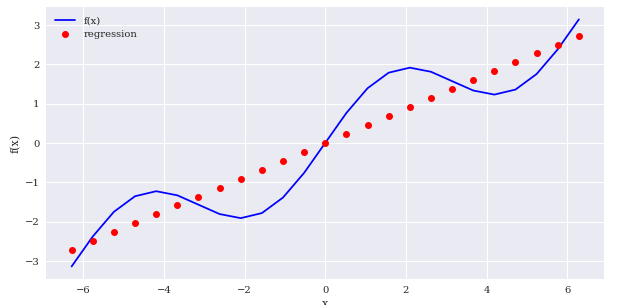
보시다시피 정확하지 않습니다.
6차식부터 조금씩 맞춰집니다.
reg = np.polyfit(x,f(x),deg=6, full=True)
ry = np.polyval(reg[0],x)
create_plot([x,x],[f(x),ry],['b','ro'],['f(x)','regression'],['x','f(x)'])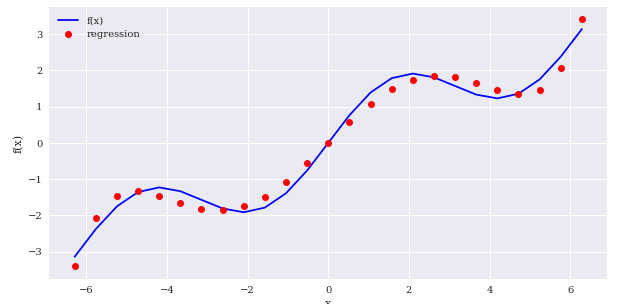
8차식정도면 거의 비슷해집니다.
#8차식
reg = np.polyfit(x,f(x),deg=8, full=True)
ry = np.polyval(reg[0],x)
create_plot([x,x],[f(x),ry],['b','ro'],['f(x)','regression'],['x','f(x)'])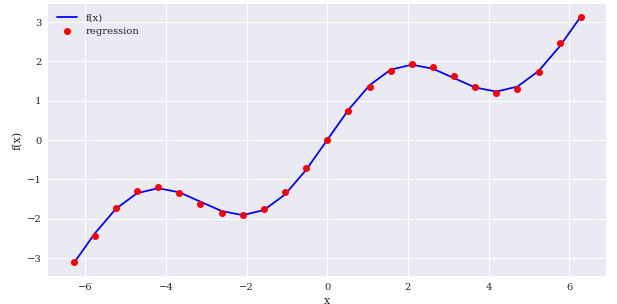
이렇듯 regression을 통해서도 데이터셋에 맞는 함수를 만들어낼 수 있습니다.
기저함수의 중요성
누구나 알고 있는 내용이지만 정리겸 더 쓰겠습니다.
결론적으로 말하면 기저함수를 무엇으로 잡느냐에 따라 상황이 달라집니다.
앞에서 보였던 f(x)는 sin함수로 이루어져 있기 때문에 기저함수를 sinx 로 놓고 시작한다면 더 정확하고 쉽게 함수를 만들어낼 수 있습니다.
파이썬에서 sinx 를 적용하려면 polyfit으로는 불가능해서 matrix로 접근해 기저함수를 각각 정하는 방식으로 가보겠습니다.
즉, b @ a = f(x) 인 행렬로 a를 구하는 문제로 보겠습니다.
b는 기저함수로 제가 정하고 그에 맞게 a만 나오면 되기 때문에 np.linalg.lstsq() 메쏘드를 사용하겠습니다.
일단 잘 나오는지 확인하기 위해 3차식으로 regression을 해보겠습니다.
matrix = np.zeros((4, len(x))) # shape (4,25)
# 기저함수 정하기
matrix[3,:] = x**3
matrix[2,:] = x**2
matrix[1,:] = x
matrix[0,:] = 1
# a 구하기
reg = np.linalg.lstsq(matrix.T, f(x), rcond=None)[0]
# 구한 a로 y값 구하기
ry = np.dot(reg,matrix)
create_plot([x,x],[f(x),ry],['b','ro'],['f(x)','regression'],['x','f(x)'])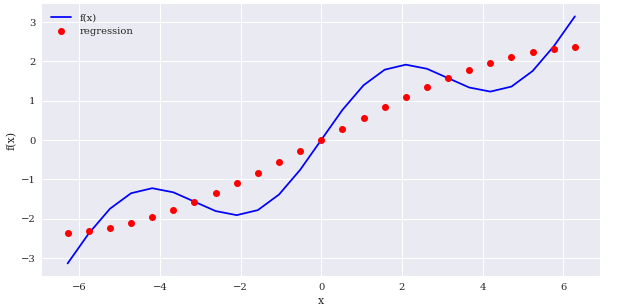
잘 되는 걸 볼 수 있습니다. 이제 4번째 기저를 sinx 로 바꾸겠습니다.
matrix[3,:] = np.sin(x)
matrix[2,:] = x**2
matrix[1,:] = x
matrix[0,:] = 1
reg = np.linalg.lstsq(matrix.T, f(x), rcond=None)[0]
ry = np.dot(reg,matrix)
create_plot([x,x],[f(x),ry],['b','ro'],['f(x)','regression'],['x','f(x)'])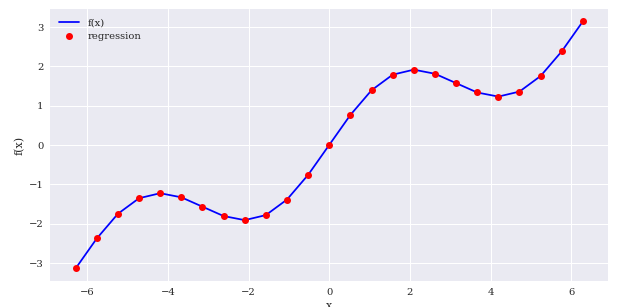
당연한 결과지만 sin(x)로 넣어놓으니 기저가 4개만 되어도 비교적 정확하게 함수를 만들어내는 걸 볼 수 있습니다.
polynomial으로 구태여 찾아내려고 한다면 기저를 9개(8차식)나 쓰고서야 지금의 결과와 비슷하게 나오기 때문에 계산비용면에서 굉장히 비효율적이라는 걸 알 수 있습니다.
이처럼 어떤 기저함수를 가지고 가느냐에 따라 시간과 계산량을 줄일 수 있기 때문에 모형에 대한 신중한 결정이 필요합니다.
하지만 잘 정돈되지 않은 데이터셋을 접한다면 좋은 기저를 찾기 힘들것입니다. 과최적화도 간과해서는 안되기 때문에 쉽지 않은 작업인 것은 분명하지만 계속해서 찾아내려고 한다면 나름의 메커니즘을 구축할 수 있을 거라 생각합니다.
포스팅은 여기서 마치고 regression에 대한 글은 추후에 더 남기도록 하겠습니다. 긴 글 읽어주셔서 감사합니다.
관련 포스팅
[수학] - [수치해석] 최소 제곱 방법(Least square approximation)
[데이터 사이언스/머신러닝 딮러닝] - [기초] 보간법(Interpolation)
[데이터 사이언스/머신러닝 딮러닝] - [Python]회귀(3D plot)
'데이터 사이언스 > 머신러닝 딮러닝' 카테고리의 다른 글
| [머신러닝] MNIST를 이용한 다중분류기 구현기 (0) | 2021.12.11 |
|---|---|
| [머신러닝] 혼동행렬(Confusion matrix) (0) | 2021.12.07 |
| [분류문제] MNIST로 이진분류기 만들기 (0) | 2021.11.28 |
| [Python]회귀(3D plot) (0) | 2021.11.03 |
| [기초] 보간법(Interpolation) (0) | 2021.10.01 |
데이터목장님의
글이 좋았다면 응원을 보내주세요!



