선형회귀(Linear regression)
- 데이터 사이언스/머신러닝 딮러닝
- 2021. 12. 20.
일차식으로 이루어진 선형회귀에 대한 내용입니다.
선형회귀는 간단한 상관관계에 대해 사용할 수 있습니다.
예를 들면, 키와 몸무게의 관계나 공부량과 성적의 관계와 같이 상관되는 특성이 단순한 경우입니다.
그래프로는 증가함수를 보여주거나 감소함수를 보여주는 경우를 의미합니다.
회귀는 과학실험을 통해 팩터를 찾고 공식을 만들어가던 것과 같이
주어진 데이터를 해석해 적당한 그래프 모양을 수학식으로써 표현해나가는 과정이라고 볼 수 있는데
그 중에서 선형 회귀는 일차식으로 이루어진 식으로 결정짓는 것을 말합니다.
이전 포스팅(회귀)는 일반화된 경우였고 기저를 정하는 것부터 시작했다면 선형회귀는 기저가 {1,x} 로만 이루어진 식으로 볼 수 있습니다.
변수(특성)의 개수가 여러개로 나타날 수 있는데 이건 스스로 판단해 1개로 제한을 할 수도 있고 변수 확장을 허용할 수도 있습니다. 구하고자 하는 것은 파라미터를 무엇으로 결정지을 것인가입니다.
물론 파라미터를 결정지을 수 없는 안맞는 식일 수도 있습니다.
그러면 기저를 변경하는 방식으로 적합한 모델을 찾아가는 과정이 필요합니다.
중고등학교때 배운 y= ax+b 를 단순 선형이라 하고 머신러닝에서는 a를 가중치(weight), b를 편향(bias) 라고 합니다. 특성을 여러개로 늘리면 다중 선형이라 합니다.
다중 선형을 식으로 나타내면 다음과 같습니다. $$ y = h_\theta(x) = \theta_0 + \theta_1x_1+\theta_2x_2+ ··· + \theta_nx_n $$
특성값은 $ x_1$~$x_n $ 이고 n개의 특성값을 갖게 됩니다.
결정지어야 할 파라미터는 $\theta_1$~$\theta_n$ 이 됩니다.
위에서 언급한 키와 몸무게의 상관관계에서 키를 y값으로 몸무게를 x값으로 넣는다면 키는 몸무게에 따라 실제로 직선의 상관관계를 보여주는지를 살펴보면 됩니다. 이때 몸무게는 키를 결정짓는 특성이라고 볼 수 있습니다.
하지만 실제로 키는 영양상태나 유전의 영향도 있기 때문에 이 부분의 대한 특성도 필요에 따라선 고려를 해주어야 합니다. 이럴 때 영양상태, 유전의 특성을 추가해서 실제적으로 비교를 할 수도 있습니다.
데이터 확보의 어려움이나 내가 얘기하고자 하는 방식이 아니라면 특성을 뺄 수도 있습니다.
순전히 분석자의 몫입니다.
수식정리
수식정리로 실제적으로 어떻게 처리를 하는지 살펴보겠습니다.
다항선형의 경우 아래와 같은 식이 나옵니다.
$$ y = h_\theta(x) = \theta_0 + \theta_1x_1+\theta_2x_2+ ··· + \theta_nx_n $$
데이터의 양이 많기 때문에 연립방정식 형태로 나타나게 됩니다. 즉, 행렬로써 표현할 수 있습니다.
$$ y = \theta ·x $$
여기서 $x = (x_0,x_1,...,x_n) $ 인 벡터이고 $x_0=1$입니다. $x_0$ 은 $\theta_0$ 과 내적곱을 한 것으로 여기는 겁니다. $ \theta=(\theta_0,\theta_1,...,\theta_n)$ 는 파라미터를 담은 파라미터 벡터가 됩니다. x는 데이터로 주어지기 때문에 $\theta$의 파라미터를 잘 구하는 것이 훈련의 목적이 됩니다. 실제값과 예측값을 줄이기 위해서는 변하는 변수인 $\theta $ 를 잘 구해야만 오차를 줄일 수 있기 때문입니다.
오차를 측정하는 함수를 비용함수(Cost function), 손실함수(Loss function) 또는 목적함수(Objective function)이라고도 합니다. 오차를 측정하는 방법이 많지만 보통 회귀에서는 MSE(mean square error)를 이용해 오차를 확인합니다.
훈련세트 X에 대한 MSE는 다음과 같습니다.
$$ MSE(X,h_\theta) = \frac{1}{m} \sum_{i=1}^{m} (\theta^Tx^{(i)} - y^{(i)})^2 $$
지금 현 문제는 행렬문제이고 최소제곱문제와 같은 상황이 되어서 구한 파라미터 $ \theta$를 바탕으로 만든 예측값과 실제값의 오차가 작아지면 됩니다. 이는 정규방정식을 통해서 구할 수 있습니다.
따라서 정규방정식을 적용하면 다음과 같이 나옵니다.
$$ \hat{\theta} = (X^T X)^{-1} X^Ty $$
최소화된 오차값이 적용된 $ \hat{\theta} $ 를 찾게 됩니다.
파이썬 구현
간단하게 데이터를 만들어서 단순 선형회귀(y=ax+b)를 정리한대로 해보겠습니다.
이해를 위해 y를 함수로 표현했습니다. 파라미터가 2와 5에 가까이 나오게 한다면 성공한 것입니다.
import numpy as np
X = 2*np.random.rand(100,1)
y = 2+5*X+np.random.randn(100,1)
from matplotlib.patches import Polygon
from pylab import plt,mpl
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'
%matplotlib inline
fig, ax = plt.subplots(figsize=(10,6))
# 그리기
plt.scatter(X,y)
plt.ylim(bottom=0)
plt.xlim(left=0)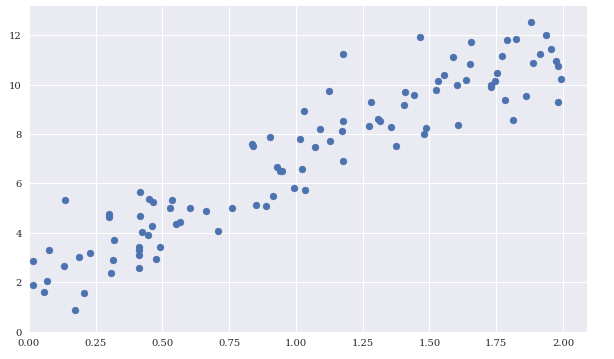
# x0=1 추가
X_ = np.c_[np.ones((100,1)),X]
#정규방정식으로 theta 구하기
theta_best = np.linalg.inv(X_.T.dot(X_)).dot(X_.T).dot(y)
print(theta_best)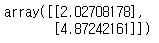
a와 b 값을 최소화하였습니다. 2와 5에 많이 가까이 가기는 했습니다.
예측값을 가지고 직선을 그려보겠습니다.
# 아무거나 점 하나
X_new = np.array([[0],[2]])
X_new_ = np.c_[np.ones((2,1)),X_new] #x0=1 추가
y_predict = X_new_.dot(theta_best)
plt.plot(X_new,y_predict,'r-')
plt.plot(X,y,'b.')
plt.show()
직선이 점 분포의 중간에 들어가기는 한것같습니다.
오차를 한번 구해봐야겠습니다.
# X_의 각각의 값을 꺼내서 theta_best와 계산후 값을 합친다
predict_value = np.array([])
for i in range(len(X_)):
predict_value = np.append(predict_value,X_[i].dot(theta_best),axis=0)
predict_value = predict_value.reshape(100,1)
from sklearn.metrics import mean_squared_error
mean_squared_error(y, predict_value)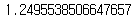
오차가 꽤 작게 나왔습니다.
선형회귀가 어느정도 완성된 것 같습니다.
성능향상
선형 회귀 같이 파라미터를 최적화 하는 알고리즘을 옵티마이저(Optimizer) 라고 합니다.
선형 회귀 모델은 굉장히 빠르게 구할 수 있는 장점이 있지만 특성이 많아지면 행렬계산을 해야하니 그만큼 느려지고 메모리 소모도 많아집니다. 그래서 복잡도가 올라가면 선형 회귀 모델로는 불가능한 상황이 발생합니다.
이런 문제를 해결하기 위한 방법으로 경사하강법을 주로 쓰는데 경사 하강법에 대한 내용은 다음 포스팅으로 미루겠습니다.
긴글 읽어주셔서 감사합니다.
관련 포스팅
[수학] - [선형대] 정규방정식(Normal equation)
[데이터 사이언스/머신러닝 딮러닝] - [Python] 회귀(Regression)
[수학] - [수치해석] 최소 제곱 방법(Least square approximation)
참고 문헌
'데이터 사이언스 > 머신러닝 딮러닝' 카테고리의 다른 글
| [머신러닝] 지도학습 성능 평가방법 총정리 (0) | 2022.12.05 |
|---|---|
| [우분투] 파이토치 설치 쉽게하기 (0) | 2022.09.06 |
| [머신러닝] MNIST를 이용한 다중분류기 구현기 (0) | 2021.12.11 |
| [머신러닝] 혼동행렬(Confusion matrix) (0) | 2021.12.07 |
| [분류문제] MNIST로 이진분류기 만들기 (0) | 2021.11.28 |