[머신러닝] 지도학습 성능 평가방법 총정리
- 데이터 사이언스 / 머신러닝 딮러닝
- 2022. 12. 5.
머신러닝은 지도학습, 비지도 학습, 강화학습 등 다양한 모델이 있습니다. 학습방법에 따라 성능에 대한 고찰도 약간씩 달라집니다. 이번 포스팅에서는 지도학습 모델에서 자주 쓰는 평가방식에 대해 정리하려 합니다.
범주형 모델 평가
범주형 모델은 분류를 목적으로 만든 모델입니다. 성능 또한 잘 분류했는지를 확인합니다. 평가를 위해서 혼동행렬(Confusion Matrix)를 이용하고 주로 F1_score나 ROC 곡선 점수로 평가를 합니다.
혼동행렬, ROC 곡선에 대한 개념에 대한 자세한 내용은 아래 포스팅에서 확인하시기 바랍니다.
[머신러닝] 혼동행렬(Confusion matrix)
이전 포스팅에서 MNIST에서 이진 분류기를 만들어 보았는데 글이 길어지다 보니 검증에 대한 개념을 위한 포스팅을 따로 합니다. 이진 분류기를 만드는 과정과 검증방법은 이전 포스팅에서 확인
seong6496.tistory.com
혼동행렬은 4가지 경우로 구성되어 있습니다.
TP(True Positive), FN(False Negative), FP(False Positive), TN(True Negative) 을 가지고 평가를 하게 됩니다.

| 평가지표 | 식 | 요약 |
| 정확도 or 정분류율(Accuracy) | TP+TNTP+TN+FP+FN | 전체 데이터 수에서 올바로 분류한 데이터 수의 비율 |
| 오류율(Error rate) | FP+FNTP+TN+FP+FN | 1-정확도. 전체 데이터 수에서 잘못 분류한 데이터 수의 비율 |
| 민감도(Sensitivity) or 재현율(Recall) or 참 긍정률(TPR) | TPTP+FN | 실제 참인 것 중에서 모델이 참이라고 예측한 비율.TR Ratio라고도 함 |
| 특이도(Specificity) or 참부정률(TNR) | TNTN+FP | 실제 거짓인 경우를 거짓으로 잘 분류하여 판정한 비율 |
| 거짓 긍정률(False Postiive Rate, FPR) | FPTN+FP | 1-특이도 실제 거짓인 값중 참으로 잘못 분류한 비율 |
| 정밀도(Precision), or PPV | TPTP+FP | 참이라고 분류한 것중에서 실제 값이 참 인 비율 |
| F1 Score | 2∗Precision∗RecallPrecision+Recall | 정밀도와 재현율의 조화평균. 0~1사이 값이 나타남. 1에 가까울수록 모델의 예측이 좋다고 볼 수 있음. |
혼동행렬 평가 구현
mnist 숫자 5 구분하는 이진분류를 기준으로 출력을 해보겠습니다.
구식 방법이긴 하지만 이진분류하는 방법은 아래 포스팅을 참고해주세요
[분류문제] MNIST로 이진분류기 만들기
머신러닝의 가장 기초중의 기초 머신러닝의 'Hello World' MNIST입니다. 머신러닝은 기본적으로 주어진 데이터를 가지고 컴퓨터를 훈련을 시키기 때문에 훈련,검증의 두단계를 거칩니다. 주어진 데
seong6496.tistory.com
위 표를 sklearn으로 구할 수 있는데 가장 간편한 건 classification_report입니다.
classification_report는 간단한 리포트로 precision, recall, f1_socre 의 점수를 볼 수 있습니다.
from sklearn.metrics import classification_report
print(classification_report(y_train_5, y_train_pred))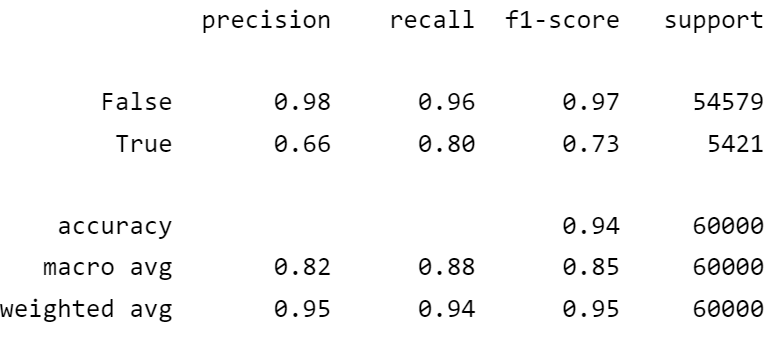
단점은 수치를 따로 쓸 수 없습니다. 말그대로 리포트입니다.
수치를 가져오고 싶다면 일일히 구해야합니다.
다행히도 정확도, 정밀도, 재현율, f1을 구하는 메쏘드가 있습니다.
특이도와 오류율,거짓긍정률은 직접 구해야합니다.
오류율과 거짓긍정률은 전체에서 값을 빼면 되므로 구한거나 다름없습니다.
특이도만 confusion maxtrix를 이용해 구합니다.
from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, f1_score, recall_score
cm = confusion_matrix(y_train_5,y_train_pred)
accuracy = accuracy_score(y_train_5,y_train_pred)
precision = precision_score(y_train_5,y_train_pred)
f1 = f1_score(y_train_5,y_train_pred)
recall = recall_score(y_train_5,y_train_pred)
specificity = cm[0,0]/(cm[0,0]+cm[0,1]) #confusion_matrix에서 직접 구해야함
error_rate = 1-accuracy
fpr = 1-specificity
print(f'accuracy:{accuracy}\nprecision:{precision}\nf1_score:{f1}\nrecall:{recall}\nspecificity:{specificity}\nerror_rate:{error_rate}\nFPR:{fpr}')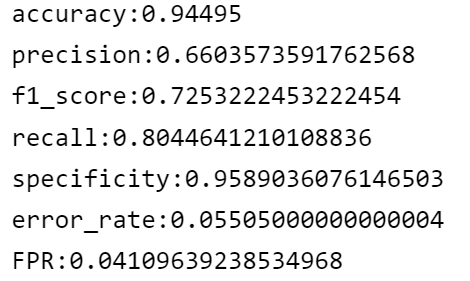
ROC 곡선
ROC곡선에 대한 개념은 이전 포스팅에서 다뤘습니다. 평가에 대한 정리만 하겠습니다.
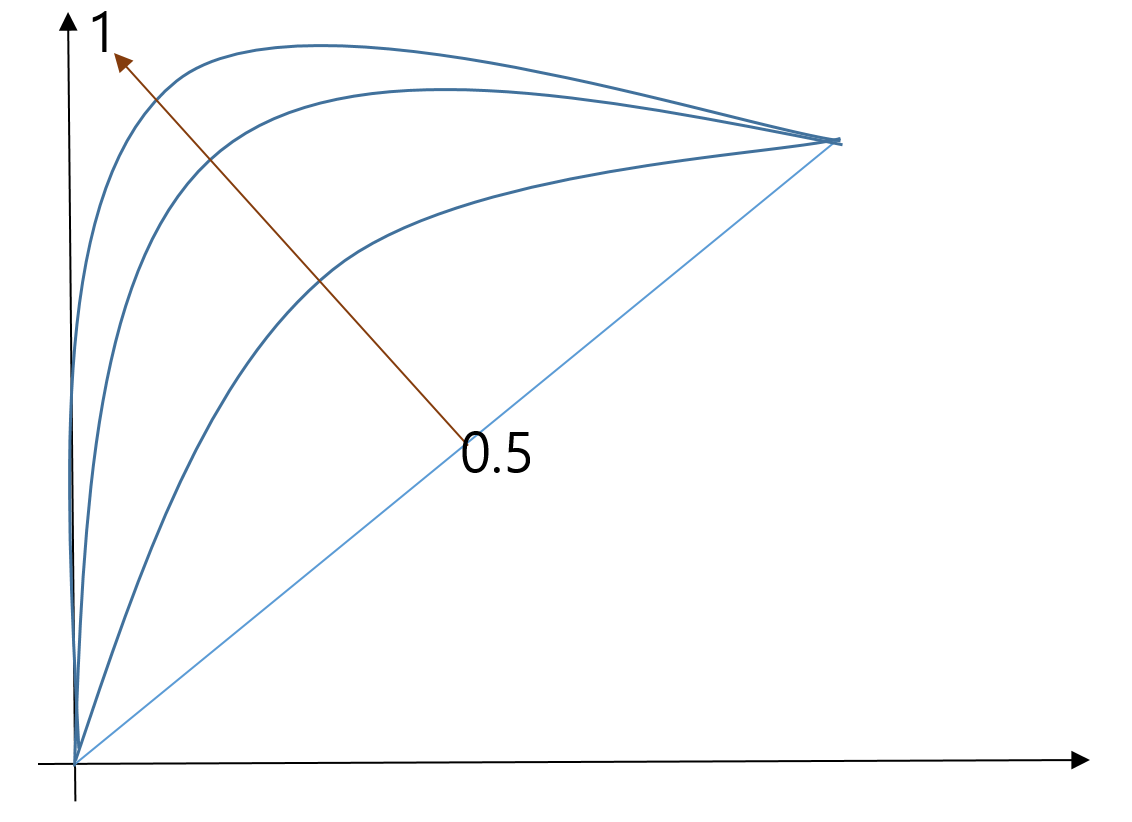
ROC는 간단합니다. 0.5~0.6은 예측이 안좋은 모델이고 0.9~1.0이면 예측이 뛰어난 모델로 볼 수 있습니다.
그런데 0.9면 과적합이 아닌가 의심해봐야합니다.
0.8~0.9 사이면 예측력이 좋은 편이면서 과적합일 확률도 낮아져서 준수한 모델일 가능성이 큽니다.
ROC 점수 구현
점수에 대한 출력만 보이겠습니다.
그래프를 그리는 방법은 아래 포스팅에서 성능검증 내용을 참고해주시기 바랍니다.
[분류문제] MNIST로 이진분류기 만들기
머신러닝의 가장 기초중의 기초 머신러닝의 'Hello World' MNIST입니다. 머신러닝은 기본적으로 주어진 데이터를 가지고 컴퓨터를 훈련을 시키기 때문에 훈련,검증의 두단계를 거칩니다. 주어진 데
seong6496.tistory.com
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_train_pred)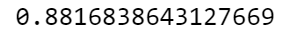
연속형 모델 평가
연속형 모델이란 정답이 분류보다는 예측에 초점을 맞춘 모델입니다. 분류 문제처럼 답이 명확하진 않기 때문에 주로 회귀분석을 합니다.회귀분석에 대한 내용은 아래 포스팅에서 다루었습니다. 참고하시기 바랍니다.
[Python] 회귀(Regression)
회귀 분석을 파이썬으로 구현(?)해보겠습니다. 회귀분석을 통해서 데이터 분석을 많이 하게 되는데요. 보통 선형 회귀 모델을 많이 쓰고 있는데 이번 포스팅에서는 일반적인 모형을 통해 전체적
seong6496.tistory.com
SST,SSE,SSR
회귀모형을 평가를 하기 위해서는 SST(Sum of Squares Total), SSE(Sum of Squares Error), SSR(Sum of Squuares Regression)에 대한 정의가 필요합니다.
만약 회귀가 일어난다면 아래와 같이 회귀선이 그려지고 실제값과 얼마나 적절하게 그려졌는지 평가합니다.
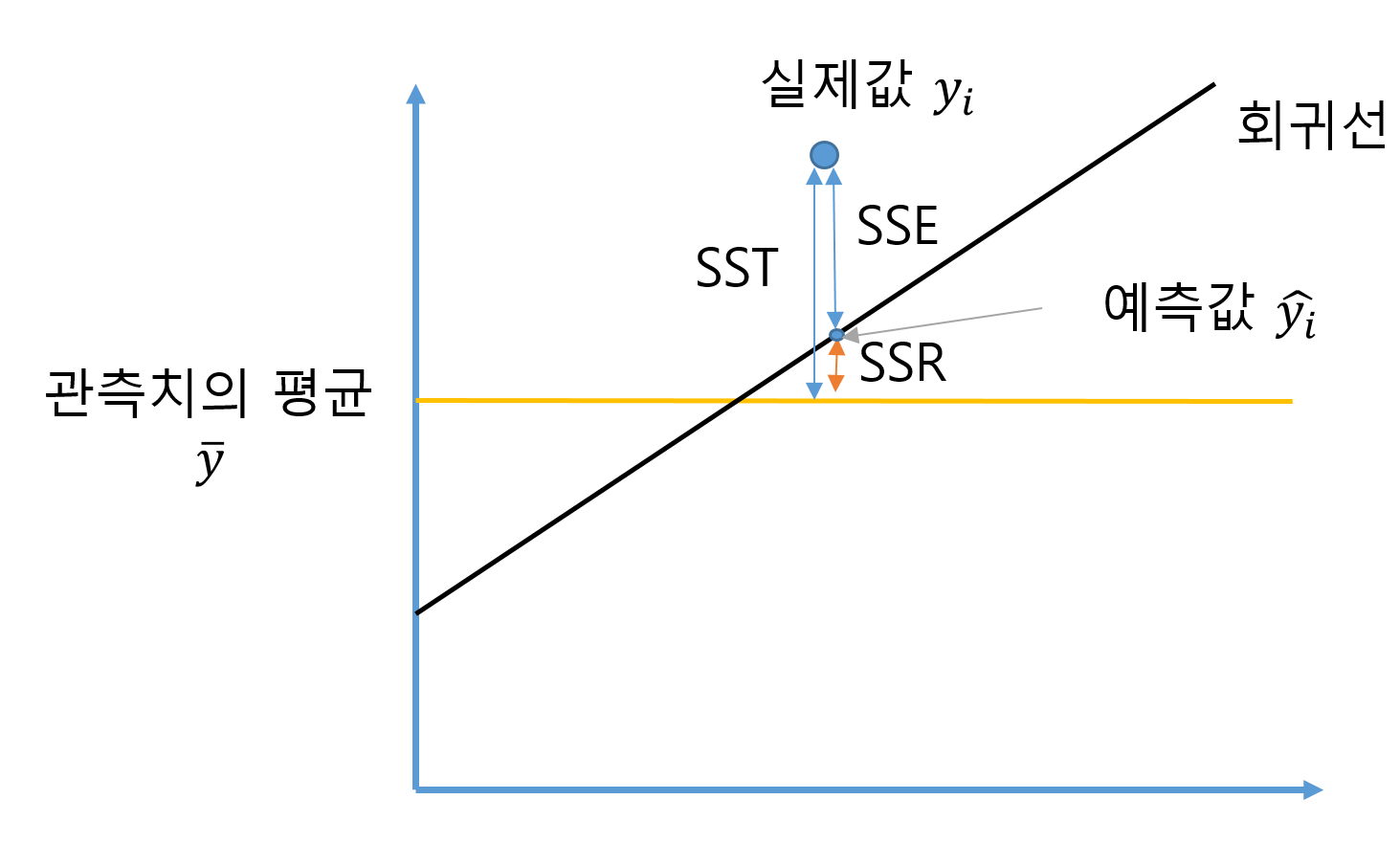
식을 보면 다음과 같습니다.
SST=n∑i=1(yi−ˉy)2
SSE=n∑i=1(yi−^yi)2
SSR=n∑i=1(^yi−ˉy)2
실제로 SSR = SST-SSE 라는 걸 시그마의 성질과 인수분해 a2−b2=(a−b)(a+b) 로 증명할 수 있습니다.
즉, 위의 그림처럼 SST = SSR+SSE 이 가능해집니다.
연속형 모델의 평가지표 정리
평가를 할 때 SSE가 직관적으로 사용하는 오차제곱합이고
상황에 따라 확인해야할 것이 달라집니다. 그에 맞게 여러 평가지표가 쓰입니다.
| 평가지표 | 식 | 요약 |
| SSE(오차제곱합) | ∑ni=1(yi−^yi)2 | 예측값과 실제값의 차이의 제곱합 회귀모형 평가시 많이 쓰인다. |
| R2_score(결정계수) | SSESST | 회귀모형의 선형도 측정 1에 가까울수록 선형으로 설명할수있다는 의미. 선형회귀분석에서 유효. 비선형회귀인경우 큰의미 없음. |
| AE(Average Error, 평균오차) | 1n∑ni=1(yi−^yi) | 예측오차의 평균 예측값이 평균 미달인지 아닌지 확인할때 쓰임 |
| MSE(Mean Squared Error, 평균제곱오차) | 1n∑ni=1(yi−^yi)2 | 예측오차 제곱합의 평균 큰 오차는 더 크게, 작은 오차는 더 작게 반영 |
| MAE(Mean Absolute Error, 평균절대오차) | 1n∑ni=1|yi−^yi| | 예측오차 절대값의 평균 오차간 상쇄 예방 |
| RMSE(Root Mean Squared Error, 평균제곱오차) |  |
MSE의 제곱근 값 MSE의 수치를 제곱근으로 보정. 식이 표준편차처럼 생김.예측이 얼마나 벗어났는지에 대한 정보 제공. 일반적인 평가지표. |
| MAPE(Mean Absolute Percentage Error, 평균절대백분율오차) |  |
실제값에 대한 오차 백분율 오차 평균의 크기가 다른 모델 비교시 사용 |
구현
sklearn에는 MSE,MAE,MAPE 메쏘드만 있고 나머지는 메쏘드를 활용하거나 직접 구해야합니다.
from sklearn.metrics import mean_squared_error, mean_absolute_error, mean_absolute_percentage_error
n = len(y_VAL)
SSE = n*mean_squared_error(y_VAL,y_pred) # MSE * n
R2 = r2_score(y_VAL,y_pred)
AE = sum(y_VAL-y_pred).mean() # 직접 구함
MSE = mean_squared_error(y_VAL,y_pred)
MAE = mean_absolute_error(y_VAL,y_pred)
RMSE = mean_squared_error(y_VAL, y_pred)**0.5 # sqrt(MSE)
MAPE = mean_absolute_percentage_error(y_VAL,y_pred)
print(f'SSE:{SSE}\nR2_score:{R2}\nAE:{AE}\nMSE:{MSE}\nMAE:{MAE}\nRMSE:{RMSE}\nMAPE:{MAPE}')
지도학습 모델 성능 평가 기준
지도학습은 분류와 예측 문제이기 때문에 정확도가 가장 중요합니다. 정확도가 높으면 예측을 잘하는 것이고 예측을 잘하면 좋은 모델이 되는 것입니다. 그런데 머신러닝은 항상 과적합의 문제가 있습니다. 내가 학습시킨 데이터셋에서만 정확도가 높다면 아무 쓸모가 없게 됩니다. 실제로 모델만으로는 100% 예측할 수 없습니다. 100% 예측력은 존재하지도 않습니다. 따라서, 정확도만 높다고 무조건 되는 건 아닙니다.
지도학습의 평가 기준은 다음과 같습니다.
- 안정성 : 같은 모집단 내에서 다른 데이터를 적용하는 경우에도 결과가 비슷하게 나오는가?
- 효율성 : 얼마나 적은 입력변수를 사용했는가?
- 정확성 : 예측과 분류의 정확도가 높은가?
- 해석력 : 입력변수와 출력변수와의 관계를 잘 설명하는가?
편향과 분산의 관계
지도학습 모델의 편향과 분산 관계를 아래 그림으로 표현해보았습니다. 아래 그림처럼 편향과 분산이 적다면 과녁 중간에 맞추는 게 가능해집니다.
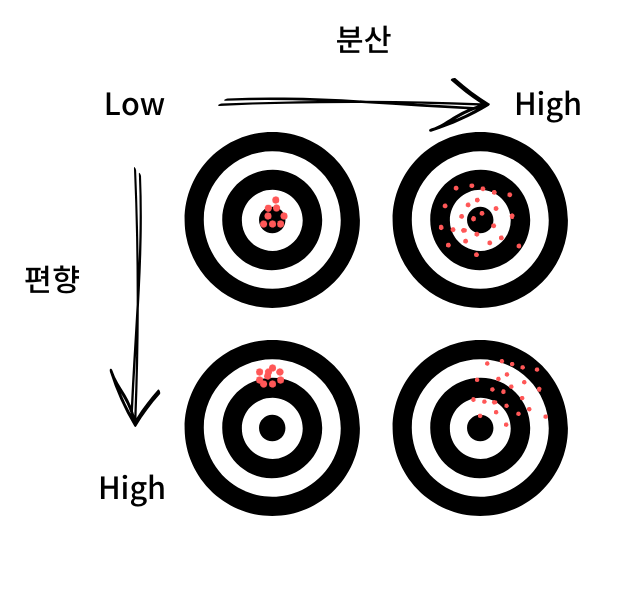
하지만, 안타깝게도 편향과 분산은 트레이드 오프(trade-off) 관계입니다. 한쪽이 증가하면 한쪽이 감소하게 되어있습니다.
즉, 한쪽을 포기하면 과대적합이나 과소적합이 되어버립니다.
모델이 복잡해지면 편향이 작아지지만 분산이 커져 과대적합이 되고, 모델이 단순해지면 편향이 커지고 분산은 작아져 과소적합에 빠질 수 있습니다.
과녁 그림처럼 정답만 맞추는 모델은 이상적인 모델일 뿐 실제로 구현하기 어렵습니다. 그럼에도 최소의 에러를 구하기 위해서 많은 모델 중 편향과 분산의 합(전체에러)가 최소가 되는 지점을 찾아서 이상적인 모델에 가깝게 만들어 가는 노력을 해야합니다.
마치며
지도학습 성능 평가방법에 대해 정리했습니다.
도움이 되셨으면 좋겠습니다.
관련 포스팅
'데이터 사이언스 > 머신러닝 딮러닝' 카테고리의 다른 글
| [자연어처리] NLTK 설치 및 소개 (0) | 2023.05.15 |
|---|---|
| iris dataset 가져오기(데이터셋 가져오는 요령) (0) | 2023.01.14 |
| [우분투] 파이토치 설치 쉽게하기 (0) | 2022.09.06 |
| 선형회귀(Linear regression) (0) | 2021.12.20 |
| [머신러닝] MNIST를 이용한 다중분류기 구현기 (0) | 2021.12.11 |
데이터목장님의
글이 좋았다면 응원을 보내주세요!



