[분류문제] MNIST로 이진분류기 만들기
- 데이터 사이언스/머신러닝 딮러닝
- 2021. 11. 28.
머신러닝의 가장 기초중의 기초 머신러닝의 'Hello World' MNIST입니다.
머신러닝은 기본적으로 주어진 데이터를 가지고 컴퓨터를 훈련을 시키기 때문에 훈련,검증의 두단계를 거칩니다.
주어진 데이터는 유한하니 데이터를 분리시켜 하나는 훈련을 시키고 다른 하나로는 검증을 시행합니다.
여기서 주의할 점은 훈련데이터와 검증데이터가 겹치면 안됩니다.
이미 훈련을 한 문제로 검증을 하면 당연히 100점이 나오기 때문에 의미가 없습니다.
적당한 훈련 끝에 데이터를 아무거나 가져와도 내가 원하는 답을 해주는지를 기대하기 때문에
주어진 환경안에서 잘 훈련되어 정확한 답을 끌어내게끔 만들어내는게 목적이라고 볼 수 있습니다.
MNIST는 손으로 쓴 숫자이미지로 이를 이용해
컴퓨터를 학습시켜 컴퓨터가 아무 숫자를 보여주면
정확하게 인지하는 하나의 기계를 만드는 작업을 하는 것입니다.
사이킷런과 텐서플로우를 이용해 위 작업을 해보겠습니다.
데이터 받기
MNIST 데이터셋은 28x28 사이즈로 되어 있고 0~9까지의 숫자로 이루어져 있습니다.
데이터를 불러오겠습니다.
이미 다들 어떻게 하는지 아는 해법이 있는 데이터기 때문에 훈련용과 검증용 데이터를 쉽게 나눌 수 있습니다.
from tensorflow.keras.datasets import mnist
(x_train,y_train),(x_test,y_test) = mnist.load_data()
변수로 다시 정리해서 말하면 x_train으로 컴퓨터가 훈련을 해서 답을 내면 y_train과 일치하는 기계를 만드는 작업이 되겠습니다.
숫자는 이렇게 생겼습니다. 28x28 크기의 흑백으로 된 손글씨입니다.
# 100개 이미지 확인
rows =10
cols = 10
for i in range(0,rows*cols):
plt.subplot(rows,cols,i+1)
plt.imshow(x_train[i],cmap='binary')
plt.axis('off')
plt.show()
타입은 ndarray, uint8로 정수형으로 이루어져 있습니다.
총 7000개의 데이터에서 6000개는 훈련용으로 1000개는 검증용으로 쓸 예정입니다.
print(type(x_train),x_train.shape)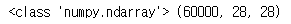
데이터 중 한개만 보면 ndarray로 이루어진 숫자로 이루어진 것을 볼 수 있습니다.
x_train[35]
이를 그림으로 보면 다음과 같이 5가 나옵니다.
plt.imshow(x_train[35],cmap='binary')
plt.axis('off')
plt.show()
이진 분류
일단 문제를 쉽게 풀어봅시다.
숫자 5가 맞는지 아닌지 분류하는 이진 분류기(binary classifier)를 만들어보겠습니다.
사이킷런에 있는 확률적 경사 하강법(SGD) 으로 할 수 있습니다.
SGD는 간단한 모델이고 이 모델을 기반으로 성능이 더 잘 나오는 모델을 적용해나가면 됩니다.
포스팅에서는 SGD로 한 예제만 보이겠습니다.
데이터 전처리
먼저 데이터 전처리를 합니다.
5가 맞는지 아닌지에 대한 boolean을 만들겠습니다.
y_train_5 = (y_train ==5) # 5 일때 True, 다른 숫자는 False
y_test_5 = (y_test == 5)
print(y_train_5)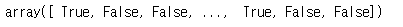
boolean을 만들었으니 x_train으로 훈련을 시켜야합니다.
하지만 현재 x_train에 숫자데이터는 2차원으로 이루어져있습니다.
x_train[35].shape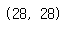
이를 1차원으로 바꿔주어야 서로 매칭이 되어 데이터를 받아들일 수 있습니다.
2차원의 숫자데이터를 1차원으로 쭉 펴주겠습니다.
x_train_reshape = x_train.reshape([-1,28*28]) #shape : (60000,784)
x_train_reshape[35].shape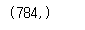
훈련
(28, 28) 을 (784,) 으로 바꿔주었고 이제 모델에 넣어서 훈련을 시켜주면 됩니다.
이미 개발된 확률적 경사 하강법(SGD) 분류기를 이용해 해보겠습니다.
사이킷런의 SGDClassifier 클래스를 사용합니다.
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(max_iter=5, random_state=42)
sgd_clf.fit(x_train_reshape,y_train_5)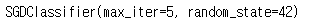
훈련이 다 되었습니다.
위에서 x_train[35]는 5였으니 확인을 해봅시다.
sgd_clf.predict([x_train_reshape[35]])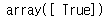
5가 맞다고 결과가 나왔습니다.
성능 검증
분류기는 오차행렬(confusion matrix)을 기반으로 보통 정밀도와 재현율로 평가를 하고
이진 분류기인 경우 ROC 곡선을 이용해 검증하기도 합니다.
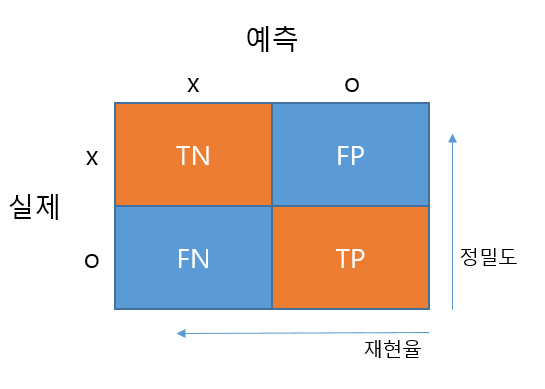
먼저 오차행렬(confusion matrix)를 만들겠습니다.
오차행렬을 그림으로 보면 다음과 같이 나타낼 수 있습니다.
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf,x_train_reshape,y_train_5,cv=3)
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5,y_train_pred)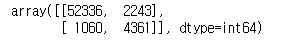
TN: 52336, TP : 4361, FP : 2243, FN : 1060 이 나왔군요.
이를 기반으로 정밀도(precision)와 재현율(recall)을 구해봅시다.
정밀도와 재현율은 다음과 같습니다.
$$ \begin{align} precision & = \frac{TP}{TP+FP} \\ recall & = \frac{TP}{TP+FN} \end{align} $$
from sklearn.metrics import precision_score, recall_score
print('precision : ', precision_score(y_train_5, y_train_pred), ' recall :', recall_score(y_train_5,y_train_pred))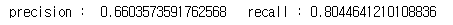
현재의 분류기는 정밀도가 약 66%, 재현율은 80% 가 됩니다.
정밀도와 재현율는 동시에 끌어올릴 수 있는 구조가 아닙니다.
그래서 $ F_1$ 점수라고 하는 하나의 숫자로 나타내는 경우가 많습니다.
$F_1$ 점수는 정밀도와 재현율의 조화평균입니다.
$$ F_1 = \frac{2}{\frac{1}{precision} + \frac{1}{recall}} $$
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)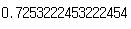
정밀도와 재현율이 비슷할수록 $F_1$ 점수가 높게 나타납니다.
그렇지만 무엇을 분류하느냐에 따라 정밀도가 중요할 수도 있고 재현율이 중요할 수도 있기 때문에 $F_1$ 점수가 높다고 좋은 분류기라고 볼 수는 없습니다.
적당한 재현율에서 정밀도를 큰 폭으로 올리는 것이 큰 관건이 되겠습니다.
이를 위해서 적당한 임계값을 살펴봐야 합니다.
어떤 임계값으로 해야 재현율 대비 정밀도를 극대화 할지 정할 수 있으니까요.
decision_function을 이용하면 각 샘풀의 점수를 얻을 수 있는데 이를 이용하여 모든 샘픔의 점수를 구한 후
모든 임계값에 따른 정밀도와 재현율의 그래프를 그려보겠습니다.
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
def plot_precision_recall_threshold(precisions,recalls, thresholds):
plt.plot(thresholds, precisions[:-1],'b--',label='precision')
plt.plot(thresholds, recalls[:-1],'g-',label='recall')
plot_precision_recall_threshold(precisions,recalls,thresholds)
plt.show()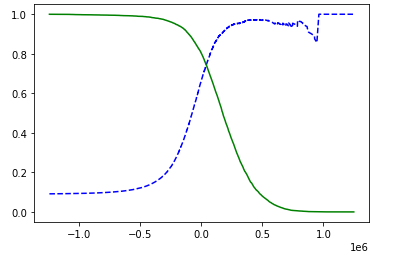
그래프에서 보듯이 재현율과 정밀도는 반대로 움직입니다.
따라서 둘다 높은 분류기 만들기는 정말 어렵습니다.
이제 적당한 재현율과 높은 정밀도를 위한 임계값을 구해보겠습니다.
90%의 정밀도에 해당하는 임계값을 찾아봅시다.
#정밀도 90% 정도의 임계값 찾기
threshold_90_precision = thresholds[np.argmax(precisions>=0.9)]
y_train_pred_90 = (y_scores>=threshold_90_precision)
#print(정밀도, 재현율)
print(precision_score(y_train_5,y_train_pred_90), recall_score(y_train_5,y_train_pred_90))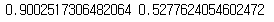
재현율이 약 52% 수준에서 90%의 정밀도를 가지는 분류기를 만들었습니다.
이번에는 수신기 조작 특정(ROC) 곡선입니다.
decision_function을 이용하면 각 샘플의 점수를 얻을 수 있는데 이를 이용해 모든 샘플의 점수를 구한 후 Roc곡선을 구합니다.
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores) #roc_curve
def plot_roc(fpr,tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0,1],[0,1],'k--')
plot_roc(fpr,tpr)
plt.show()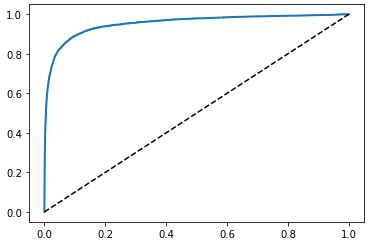
파란색 곡선이 점선에서 멀리 떨어져 왼쪽 위 모서리 쪽으로 많이 가면 갈수록 좋은 분류기입니다.
이제 곡선 아래의 면적(AUC)를 구해 즉, 수치로써 구해 다른 분류기들과 비교를 할 수 있습니다.
완벽할수록 AUC가 1에 가깞고 완전한 랜덤 분류기는 0.5가 됩니다.
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)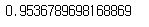
긴 글 읽어주셔서 감사드리고 이상으로 머신러닝의 기초 MNIST의 이진분류기 만드는 법에 대해 살펴보았습니다.
결과만 제시한 오차행렬에 대한 개념에 대한 포스팅을 하였습니다. 참고해주세요~!
관련 포스팅
[데이터 사이언스/머신러닝 딮러닝] - [ML] 오차행렬
'데이터 사이언스 > 머신러닝 딮러닝' 카테고리의 다른 글
| [머신러닝] MNIST를 이용한 다중분류기 구현기 (0) | 2021.12.11 |
|---|---|
| [머신러닝] 혼동행렬(Confusion matrix) (0) | 2021.12.07 |
| [Python]회귀(3D plot) (0) | 2021.11.03 |
| [Python] 회귀(Regression) (0) | 2021.10.30 |
| [기초] 보간법(Interpolation) (0) | 2021.10.01 |